Particle-hole Symmetry
There is another symmetry that has a strong influence on topology: particle-hole symmetry. It shows up in superconducting systems. As an example, imagine bringing our quantum dot in contact with a superconductor, like this:
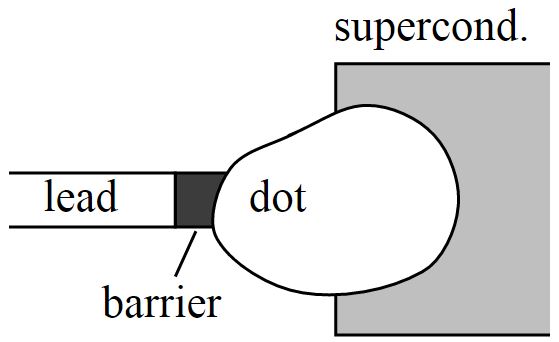
A superconductor will create and annihilate pairs of electrons by breaking apart Cooper pairs and forming them. This results in a Hamiltonian:
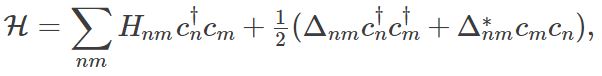
where c†n,cncn†,cn are the creation and annihilation operators of the electrons. We recall that these operators anticommute, obeying the relations cncm+cmcn=0cncm+cmcn=0 and c†ncm+cmc†n=δmncn†cm+cmcn†=δmn, where δmn=0δmn=0 if m≠nm≠nand 11 if m=nm=n.
The HH-term is the dynamics of the electrons in the dot, while ΔΔ describes the pair creation and annihilation. The matrix ΔΔ is antisymmetric because the fermion operators anticommute. Now HH does not conserve the number of electrons, but still conserves the parity of the number of electrons, that is whether the number of electrons is even or odd. We can now group all the creation and annihilation operators in a vector, C=(c1,…,cn,c†1,…,c†n)TC=(c1,…,cn,c1†,…,cn†)T. Then we write HH in the form ‘row multiplies matrix multiplies column’:
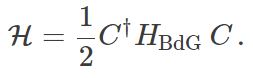
The matrix HBdGHBdG is known as the Bogoliubov-de Gennes Hamiltonian, and it has the following structure:
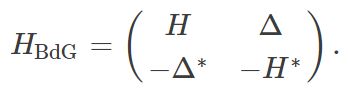
The Bogoliubov-de Gennes Hamiltonian acts on wave functions whose first half is composed out of annihilation operators of electrons, and the second half out of creations operators of the same electrons. We can think of them as annihilation operators of an extra set of holes, so that we double the amount of degrees of freedom in the system.
Since holes are related to the electrons, HBdGHBdG automatically has an extra symmetry. This symmetry exchanges electrons with holes, and has an antiunitary operator P=τxKP=τxK, where the Pauli matrix τxτx acts on the particle and hole blocks. We have that:
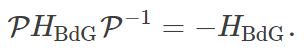
Particle-hole symmetry is represented by an anti-unitary operator which anti-commutes with the Hamiltonian (compare this situation with that of time-reversal and sublattice symmetries). Because of the minus sign in the particle-hole symmetry, the spectrum of HBdGHBdG must be symmetric around zero energy (that is, the Fermi level). Indeed, for every eigenvector ψ=(u,v)Tψ=(u,v)T of HBdGHBdG with energy EE, there will be a particle-hole symmetric eigenvector Pψ=(v∗,u∗)TPψ=(v∗,u∗)T with energy −E−E.
FERMI LEVEL CROSSINGS IN A RANDOM BOGOLIUBOV-DE GENNES HAMILTONIAN
Let’s generate a random Bogoliubov-de Gennes Hamiltonian HBdGHBdG:
I am text block. Click edit button to change this text. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
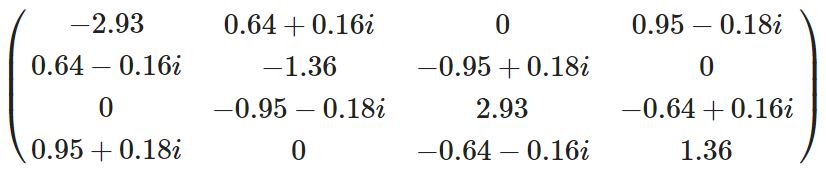
We can now see what happens when we deform it into a second one. You can indeed see clearly that the spectrum is mirrored around the line E=0E=0, just like it was in the presence of sublattice symmetry.
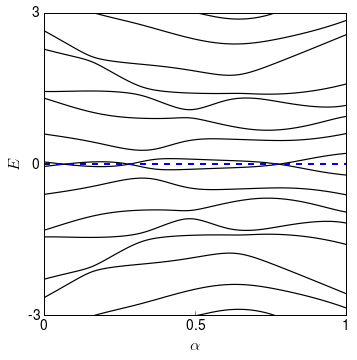
You can however notice that, unlike in the case of sublattice symmetry, energy levels do not repel around zero energy, so that crossings at zero energy appear.
FERMION PARITY SWITCHES
Let’s think a bit more about these crossings. At first, they might look a bit mysterious. In general a crossing between energy levels happens in the presence of a conserved quantity, and our random Bogoliubov-de Gennes Hamiltonian does not seem to have an obvious one. Let’s however recall what we said earlier: While the mean-field Hamiltonian of a superconductor does not conserve the number of particles, it conserves the parity of this number. In other words, forming and breaking Cooper pairs does not affect whether the superconducting quantum dots contains an even or odd number of electrons. In short, fermion parity is a conserved quantity (provided that isolated electrons do not enter or leave the dot, a possibility which we will disregard).
The above observation reveals that the existence of crossings is due to the fermion parity conservation. Fermion parity, however, is a many-body quantity, which cannot be directly described in terms of the single particle picture of the Bogoliubov-de Gennes Hamiltonian. To understand the existence of the crossings, recall that to obtain a Bogoliubov-de Gennes description of the superconductor we had to double the number of degrees of freedom by introducing holes. Hence, unlike in the case of sublattice symmetry, a pair of ±E±E energy levels does not corresponds to two distinct quantum states, but to a single quantum state. This quantum state is a coherent superposition of electrons and holes – a Bogoliubov quasiparticle: it has an excitation energy EE, and it is created by an operator a†=uc†+vca†=uc†+vc. Populating the partner state at energy −E−E is the same as emptying the positive energy state.
When a pair of levels crosses zero energy, the excitation energy EE of the Bogoliubov quasiparticle changes sign and it becomes favorable to add a Bogoliubov quasiparticle to, or remove it from the superconducting quantum dot. In other words, at each crossing the fermion parity in the ground state of the dot changes from even to odd, or vice versa. Hence these crossings are fermion parity switches.
Since the ground state fermion parity is preserved by the superconducting Hamiltonian if there are no Bogoliubov quasiparticles crossing zero energy, the ground state fermion parity is the topological invariant of this system. It is clear however that this invariant is of a different nature than the one of the non-superconducting systems, which is given by the number of negative eigenvalues of the Hamiltonian. The latter cannot change for a Bogoliubov-de Gennes Hamiltonian, which has a symmetric energy spectrum, and hence it is not suitable to describe changes in fermion parity. Is there a way to compute this new invariant directly from the Bogoliubov-de Gennes Hamiltonian?
THE PFAFFIAN INVARIANT
In order to introduce the new invariant, we have to start with a basis transformation, that makes the Hamiltonian an antisymmetric matrix. We use the following unitary transformation in particle-hole space,
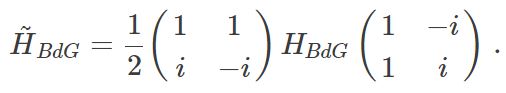
We then have
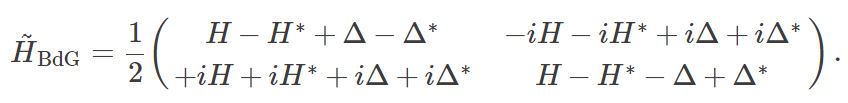
We already know that the pairing matrix ΔΔ is antisymmetric. Since HH is Hermitian H−H∗H−H∗ is also antisymmetric and H+H∗H+H∗ is symmetric. Then we can see that H~BdGH~BdG is antisymmetric.
There is a special number that we can compute for antisymmetric matrices, the Pfaffian. Its rigorous definition is not important for our course. The basic idea is simple: The eigenvalues of antisymmetric matrices always come in pairs. In the case of our H~BdGH~BdG, these are the energy eigenvalues ±En±En. By taking their product we obtain the determinant of the matrix, equal to ∏n(−E2n)∏n(−En2). The key property of the Pfaffian is that it allows to take a square root of the determinant, equal to ±i∏nEn±i∏nEn, in such a way that the sign of the product is uniquely defined. At a fermion parity switch a single EnEn changes sign, so the Pfaffian changes sign as well (while the determinant stays the same).
This feature of the Pfaffian really makes it what we are looking for. Let’s try out the sign of the Pfaffian as our topological invariant QBdGQBdG:
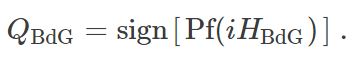
We have included a factor of ii just for convenience, so that the Pfaffian is a real number.
Whenever we need to compute a Pfaffian we just use the Pfapack package that calculates Pfaffians for numerical matrices. Let’s use that package and check that the Pfaffian indeed allows us to calculate the fermion parity of the ground state of HBdGHBdG.
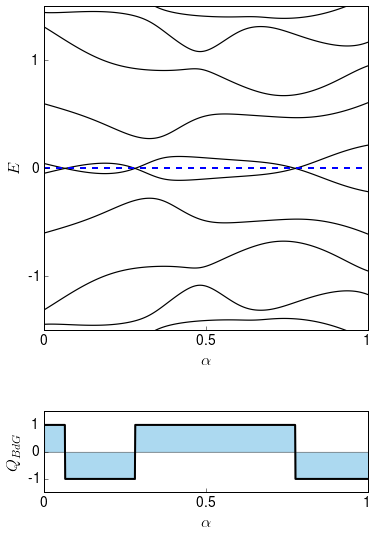
You can see how the Pfaffian invariant QBdGQBdG changes its value from +1+1 to −1−1 at every zero-energy crossing. This means that it is the correct expression for the ground state fermion parity and for the topological invariant.
Question
What happens to the topological invariant if we take the superconducting Hamiltonian and set Δ=0?



