BULK TOPOLOGICAL INVARIANT

Now that we understand the topological transition in more detail, let’s go back to the bulk Hamiltonian H(k) of the Kitaev ring and try to generalize our Dirac-equation based criterion for Majorana modes. In our effective Dirac model it was easy to identify a quantity, the mass parameter m, whose sign determined whether the system could support unpaired Majorana modes at its ends. Let’s now try to turn this effective description into a bulk topological invariant which can be computed directly from H(k). We will not attempt to give a rigorous derivation of the bulk invariant – a task which is often difficult even for advanced researchers in the field – but rather to arrive at it in a heuristic manner.

We can start with some important clues. On the one hand, we are studying a Bogoliubov-de Gennes Hamiltonian, and we have already learned that quantum dots with particle-hole symmetry are characterized by a topological invariant, the sign of the Pfaffian, which changes sign at every gap closing. On the other hand, we have just seen that the gap closing in the Kitaev chain model is accompanied by a change of sign of m. This suggests to try to link the quantity m to a Pfaffian. How to do so?

In fact, you can think of the full HBdG as a very large matrix with particle-hole symmetry. It can be put in antisymmetric form and we can compute its Pfaffian. This Pfaffian may change only when an eigenvalue of H(k) passes through zero. Because of particle-hole symmetry, for every eigenvalue E(k) we have one at −E(−k). So if E(k) passes through zero, also its partner does. Furthermore, the spectrum has to be periodic in the Brillouin zone, which means that gap closings at finite momentum always come in pairs, and cannot change the Pfaffian. There are only two points which make exception: k=0 and k=π, which are mapped onto themselves by particle-hole symmetry. In fact, for these points we have:

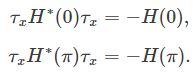
So H(0) and H(π) can always be put individually in antisymmetric form, and we can always compute their Pfaffian. Also, note that these are precisely the points in momentum space where the gap closes: at k=0 for μ=−2t and at k=π for μ=2t. All things considered, we have a strong reason to focus exclusively on H(0) and H(π). Following the procedure that we learned in the last chapter, we can therefore put H(0) and H(π) in antisymmetric form,

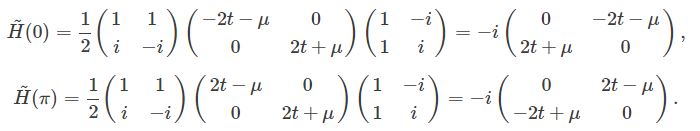
We now easily obtain that

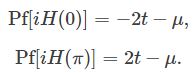
You see that the Pfaffian of H(0) changes sign at μ=−2t, and the Pfaffian of H(π) does so at μ=2t, in perfect agreement with the position of the gap closing in the band structure:

Individually, the two Pfaffians account for one of the two bulk gap closings which can occur in the model. To obtain a single bulk invariant Q we can simply multiply the two! Hence we arrive at the following expression:

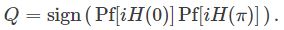
A value Q=−1 means that the bulk is in a topological phase, such that if the wire was cut at a point, two unpaired Majorana modes would appear at the ends of it. On the other hand, a value Q=+1 means that the bulk is in the trivial phase. Again, you might think that this expression for Q, that we have just cooked up, is only valid for the particular model that we are considering. However, you would be wrong:

CONNECTING THE BULK INVARIANT AND THE EDGE MODES

At the moment, the bulk topological invariant Q defined above might look just like an abstract mathematical object. We know that Q=−1 corresponds to the topological phase, but can we give a more concrete physical meaning to this value? This is the goal of this last part of the lecture.

We have already connected the Pfaffian of a Bogoliubov-de Gennes Hamiltonian to a physical quantity: The ground state fermion parity of the system. Our one-dimensional invariant involves the product of two Pfaffians, Pf[iH(0)] and Pf[iH(π)]. By taking their product we are somehow comparing the fermion parity of the two states of the chain with k=0 and k=π, and we have that Q=−1 if and only if the two parities are different.

This means that if we continuously deform H(0) into H(π) in some way without breaking the particle-hole symmetry, we must encounter a zero-energy level crossing in the energy spectrum, what we called a fermion parity switch in the last chapter.

In practice, this can be done in the following way. Let’s imagine that we change the boundary conditions of a Kitaev ring with N sites from periodic to antiperiodic boundary conditions, that is from ⟨k|n=0⟩=⟨k|n=N⟩ to ⟨k|n=0⟩=−⟨k|n=N⟩. This means that the allowed values of momentum shift from k=2πp/N to k=2πp/N+π/N.

Let’s now ask what is the difference in ground state fermion parity of the two chains. The value k=0 is always present in the chain with periodic boundary conditions, while k=π is in the first set if N is even and in the second set if N is odd. This means that in either case, the difference in the ground state fermion parities between the chains with periodic and antiperiodic boundary conditions is equal to Q!

To verify this statement, we will now physically change the boundary condition in real space. For simplicity, we will do so for a Kitaev ring with Δ=t. You will remember that, in the Majorana basis, this corresponds to the limit where neighboring Majoranas from different sites are coupled by hopping of strength t.

To go from periodic to antiperiodic boundary condition, we can change the hopping on the last bond of the ring (the one connecting sites n=N−1 and n=0) from t to −t. This can easily be done continuously and without breaking particle-hole symmetry, for instance by setting the last hopping to be equal to t(1−2λ) and varying λ in the interval [0,1], as shown in this picture:

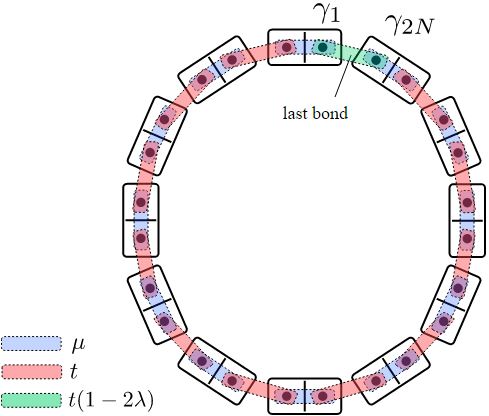
You can check that the Bogoliubov-de Gennes Hamiltonian of this closed ring satisfies particle-hole symmetry at every value of λ. Let’s now look at the energy spectrum E(λ) of the system as we vary μ from 0 to 4t, passing once again through the gap closing at μ=2t.

You can see that for μ<2t, the energy spectrum shows a zero-energy level crossing at λ=1/2. The fermion parity of the system is therefore different at λ=0 and λ=1. When λ=1/2 the hopping on the last bond is equal to zero. We have introduced a “cut” to the system, such that our closed Kitaev ring is effectively transformed to an open Kitaev chain. Because we are in the topological phase, this open Kitaev chain has two zero-energy unpaired Majorana modes!

On the other hand, when μ>2t no zero-energy level crossing is present. The ground state fermion parity is the same at λ=0 and λ=1. In this case, when we cut the system at λ=1/2, we find no unpaired Majorana modes, consistent with our knowledge of the behavior of the open chain in the trivial phase.

We have therefore learned the essence of the bulk-boundary correspondence: A non-trivial value Q=−1 of the bulk invariant for the closed chain implies the existence of unpaired Majorana modes for the open chain. Also, we have been able to connect the value of the bulk invariant to a measurable quantity, in this case the ground state fermion parity of the closed chain.

Question