In case we are interested in the linear trend of sea level rise, we have found that the observation equation for an individual tide gauge observation \(y_i\) would be:

\( y_i = l_0 + r\cdot \Delta t_i \)

with \(\Delta t_i\) the time differences with respect to \(t_0\), and the unknown initial sea level \(l_0\) at \(t_0\) and the unknown rate of change \(r\).

The figure shows the record of sea level observations (light blue) based on tide gauge observations, together with 3 'fitted' lines to model the sea level rise as a linear trend.

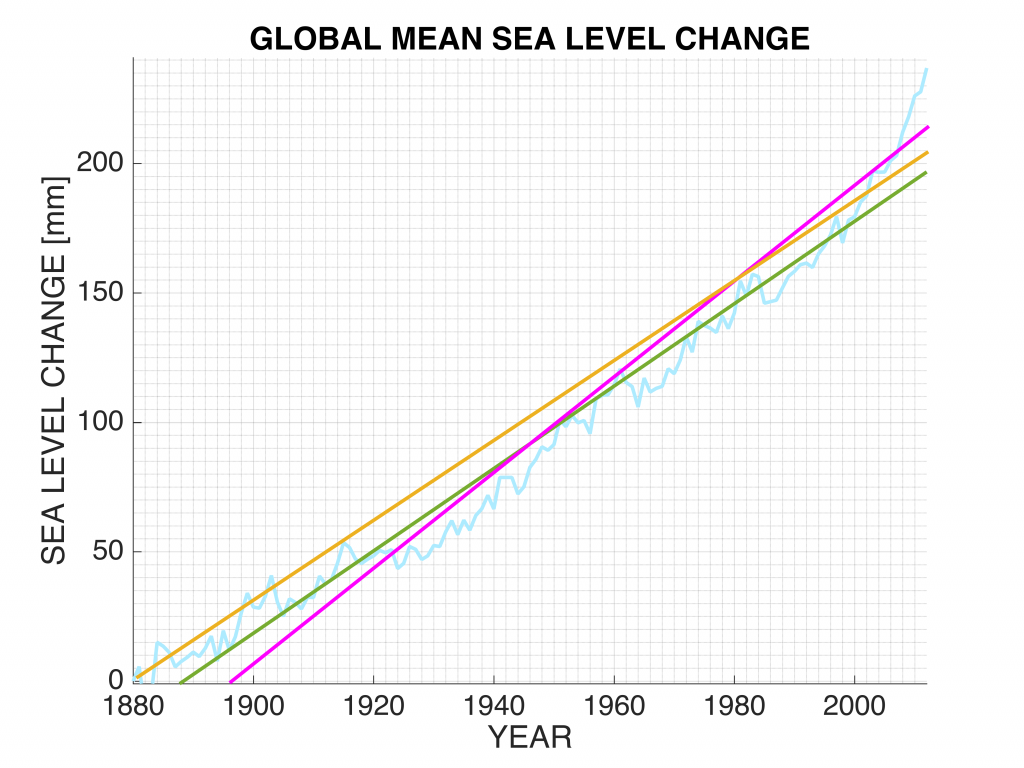
None of these lines fits perfectly to the data, this is due to measurement errors and model imperfections (the sea level variations cannot be simply modeled by a linear trend only). How to deal with this, is the topic of the upcoming parts in this course.

Food for Thought questions to you:

• - Which line ‘fits’ best to the data?
• - What criterion would you use to answer the previous question?
• - How to compute the parameters \(l_0\) and \(r\) for the ‘best fitting’ model?

In this module you will learn how the least squares principle can be used to answer these questions; we'll address them again at the end of this module.