The Bernoulli Equation

Welcome to the second optional content of this module! Here, we will take a closer look at why pressure decreases as air accelerates, and we will derive Bernoulli’s Principle from simple high school mathematics. As always, if math and physics aren’t your things, feel free to skip ahead.

As Prof. Hoekstra explained in the past lecture, moving air has a lower static pressure than stationary air, and the faster the air goes, the lower the pressure. In fact, you can try this yourself: grab two sheets of paper, hold them a few centimetres apart, and gently blow some air between them. Contrary to what you might expect, the sheets will move together! This happens because the accelerated air from your mouth has a lower static pressure than the atmosphere on the outside of the paper.

Bernoulli’s Principle was first described by Daniel Bernoulli in his book Hydrodynamica in 1738, and the later mathematical formulation was given by Leonhard Euler in 1752. Bernoulli’s Principle describes the decrease in pressure when the speed of a fluid flow increases. Note that it is only valid for so-called isentropic flows: flows where lossy effects such as turbulence and changes in temperature can be neglected, such as the smooth flow around an airfoil!

It is possible to derive the Bernoulli Equation from a variety of natural laws. Here, we will start from Newton’s Second Law, or as we state it in engineering:

Force is equal to mass times acceleration.

 

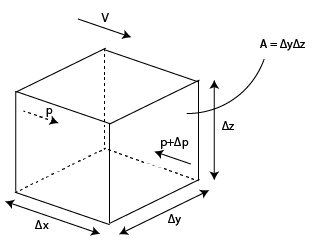
Consider an arbitrary volume of air, such as shown in the illustration. This cube with dimensions Δx by Δy by Δz is located in an airstream with velocity V. On the side where the flow comes in, it is subjected to pressure p, and on the side where the air goes out, it is subjected to pressure p + Δp . It follows that the mass of air inside the cube is simply:

We can therefore write Newton’s second law for the force in the x-direction as:

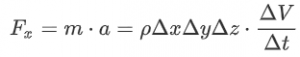
Force is equal to pressure time area or in other words: the net force on the cube is the area of the back of the cube times the pressure on the back of the cube, minus the area of the front of the cube times the pressure on the front of the cube:

And as we can see from geometry, A= ΔyΔz , therefore:

If we equate these two results, we find:

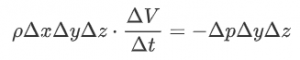
The Δy and Δz cancel out:

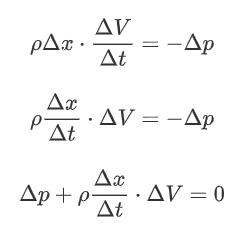
Note that Δx/Δt  is simply V:

Now, we are going to make a very important assumption. We are going to assume that the density ρ is a constant. Note that this is not true in real life! Compressibility effects are commonly seen as one approaches the speed of sound, and as such for airplanes flying at cruising speeds (typically at Mach 0.7 – Mach 0.9), this assumption does not hold. It is however very close to correcting for lower speeds, and the error increases as the speed increases. This assumption allows us to make the following manipulation:

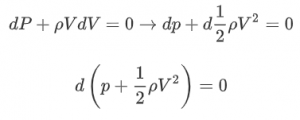
And therefore:

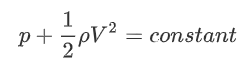
Wow! What a nice equation! As we can see, if we know the total pressure (the pressure when the fluid is not moving), we can very simply calculate the pressure when the fluid moves at a certain velocity, only knowing the density and velocity of the fluid, and not needing any other properties such as volume or properties of the gas.