A simple program performs a series of operations to obtain some desired result. In distributed systems, these operations are performed by multiple machines communicating through unreliable network environments. While the system is running, machines must coordinate to operate correctly. For example, the system may need to agree on whether a certain action happened – to reach a consensus on this question.

Consensus is the important coordination problem we discuss in this section, based on material created by Jesse Donkervliet for the Distributed Systems course at Vrije Universiteit in Amsterdam.

What is Consensus?

Consider a distributed key-value store that uses replication (see also Section 2.2.5, on Replication). Users submit read and write operations to whichever process is closest to them, reducing latency. To give the user the illusion of a single system, the processes must agree on the order to perform the queries, and especially keep the results of writing (changing) data and reading data in the correct order. Using clock synchronization techniques could work for this, but the cost of having each machine in the distributed system ask each other about whether the operations they received lead to some other order, for each operation, is prohibitively expensive in both resources and time. Another class of techniques needs to focus on the consensus problem.

In a distributed system,

Consensus is the ability to have all machines agree on a value. Consensus protocols ensure this ability.

For a protocol to ensure consensus, three things have to happen. First, the system as a whole must agree on a decision. Second, machines do not apply decisions that are not agreed upon. Third, the system cannot change a decision. Consensus protocols (distributed algorithms) can create a total order of operations by repeatedly agreeing on what operation to perform next.

 

Why Consensus is impossible in some Circumstances

Theoretical computer science has considered for many decades the problem of reaching consensus. When machine failures can occur, reaching consensus is surprisingly difficult. If the delay of transmitting a message between machines is left unbound, it is proved that, even when using reliable networks, no distributed consensus protocol is guaranteed to complete. The proof itself is known as the FLP proof, after the acronym of the family names of its creators. It can be found in the aptly named article “Impossibility of Distributed Consensus with One Faulty Process” [1]. Below we sketch its proof, through an intuition, for why it is impossible to guarantee that a consensus algorithm completes in a bounded time.

Consider that the claim is not true: There exists a consistency protocol, a distributed algorithm that always reaches consensus in bounded time. For the algorithm to be correct, all machines that decide on a value must decide on the same value. This prevents the algorithm from simply letting the machines guess a value. Instead, they need to communicate to decide which value to choose.

This communication is done by sending messages. Receiving, processing, and sending messages makes the algorithm progress toward completion. At the start of the algorithm, the system is in an undecided state. After exchanging a certain number of messages, the algorithm decides. After a decision, the algorithm – and the system – can no longer “change its mind.” The FLP proof shows that there is no upper bound on the number of messages required to reach consensus.

We now move to the core of the intuitive proof.

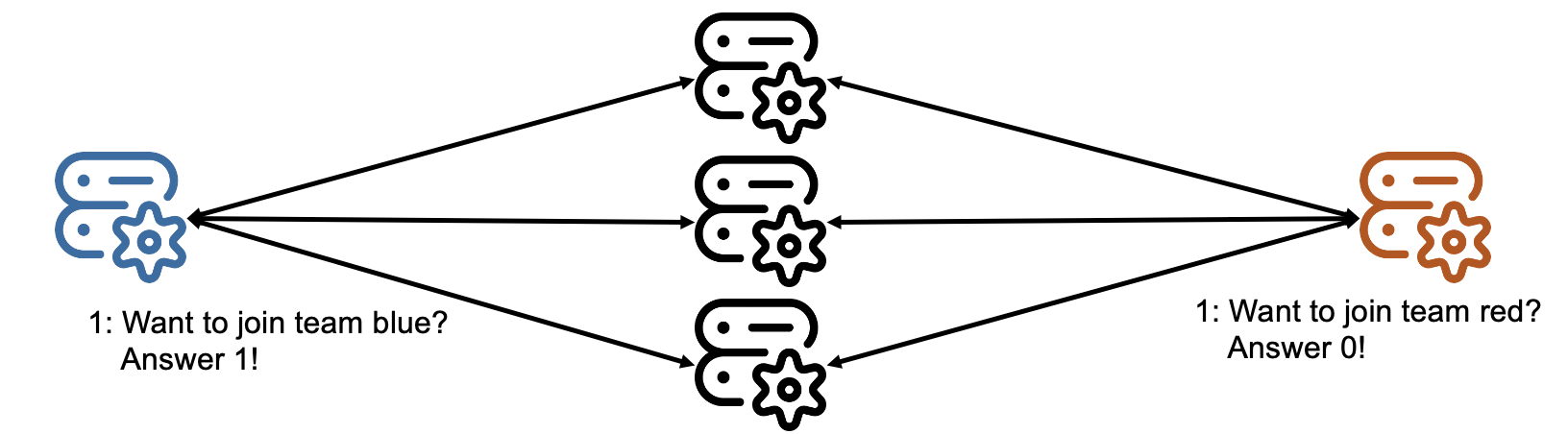
Figure 1. The consensus problem.

Imagine the consensus problem illustrated by Figure 1: A simple consensus algorithm in which machines agree which team is more popular, the blue team – system agrees on value 1 -, or the red team – system agrees on the value 0. One of the machines asks all machines, including itself, for their vote. Once it receives a majority vote for one of the values, it decides on which value the system agrees on, and sends a message to all other machines announcing the result to prevent any misunderstandings.

In Figure 1, in the beginning (marked with “1:”), each machine is about to answer. Can they reach consensus under the assumption that machines can fail and messages can be delayed indefinitely?

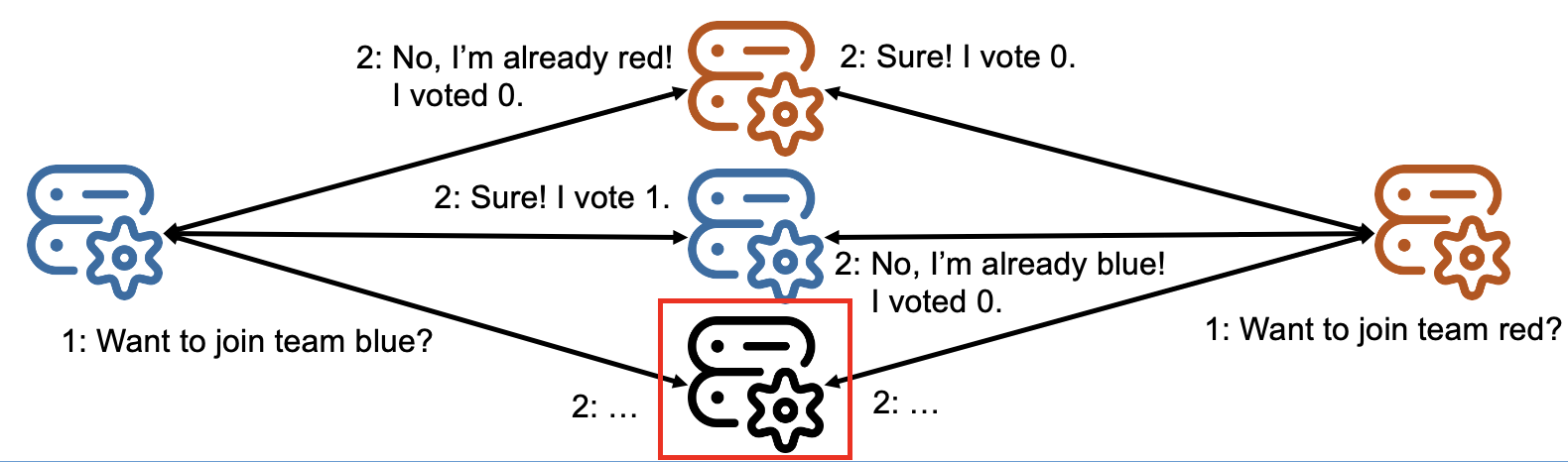
Figure 2. A problem possibly faced by every consensus protocol.

Figure 2 shows one of the key problems that can occur under the assumptions. After receiving the votes, the highlighted machine is taking a long time to announce the result.  If the algorithm waits indefinitely for this announcement, the algorithm will never reach consensus if it turns out that the machine has failed. Instead, the algorithm should, at some point, assume the machine failed and take the necessary steps to work around the failure. For example, the system chooses a new machine to take the vote.

But, just as the system has reached its decision to start calling for a new attempt to reach consensus, without the machine it considers failed, the system observes the machine did not experience a failure; instead, it was just a network delay that prevented its messages from reaching the other machines in the system. It is now too late to achieve consensus based on the previous votes, because the new consensus round has started.

The new consensus attempt starts, but again a machine can fail or be delayed. There simply isn’t a way to decide which, when failures stop the machines and delays stop their communication, possibly indefinitely.

The FLP proof [1] shows that this behavior is not specific to any algorithm. Regardless of the ingenuity of the consensus algorithm, it can always be prevented from taking a decision by delaying certain messages.

 

Impact of the FLP proof on distributed systems in practice: Many theoretical results rely on strong assumptions. In practice, many of these assumptions do not hold, so distributed systems can continue to operate. Although the FLP proof shows that a consensus protocol can always be prevented from taking a decision given the possibility of single-machine failure, it does not show that it will be prevented from making a decision. In practice, in distributed systems consensus protocols can tolerate even multiple concurrent machine failures. How? This is the topic of the next section.

 

References:

[1] The “FLP” paper: Michael J. Fischer, Nancy A. Lynch, Mike Paterson (1985) Impossibility of Distributed Consensus with One Faulty Process. J. ACM 32(2).

General Consensus and an Approach to Reach It

To achieve consensus, consensus protocols must have two properties:

1. Safety, which guarantees “nothing incorrect can happen”. The consensus protocol must decide on a single value, and cannot decide on two values, or more, at once.
2. Liveness, which guarantees “something correct will happen, even if only slowly”. The consensus protocol, left without hard cases to address – for example, no failures for some amount of time -, can and will reach its decision on which value is correct.

 

Many protocols have been proposed to achieve consensus, with various degrees of capability under various forms of failures, messaging delays they tolerate, etc. None can do so under the exact assumptions the FLP proof considers, but, for example, in practice tolerance for unbound messaging delays does not seem necessary – most operations on data take a short amount of time to complete. Among the protocols that are used in practice, Paxos, multi-Paxos, and more recently Raft seem to be very popular. For example, etcd is a distributed database built on top of the Raft consensus algorithm. Its API is similar to that of Apache ZooKeeper (a widely-used open-source coordination service), allowing users to store data in a hierarchical data-structure. Etcd is used by Kubernetes and several other widely-used systems to keep track of shared state.

 

We sketch here the operation of the Raft approach to reach consensus [1]. Raft is a consensus algorithm specifically designed to be easy to understand. Compared to other consensus algorithms, it has a smaller state space (the number of configurations the system can have), and fewer parts.

Figure 3. Raft overview.

 

Figure 3 gives a Raft overview. There are four main components:

1. Raft first elects a leader (“leader election” in Figure 3). The other machines become followers. Once a leader has been elected, the algorithm can start accepting new log entries (data operations).
2. The log (data) is replicated across all the machines in the system (“log replication” in the figure).
3. Users send new entries only to the leader.
4. The leader asks every follower to confirm. If most followers confirm, the log is updated (performs the operation).

 

We describe three key parts of Raft. These do not form the entirety of Raft, which is indicative that even a consensus protocol designed to be easy to understand still has many aspects to cover.

The Raft leader election: Having a leader simplifies decision-making. The leader decides on the values. The other machines are followers, accepting all decisions from the leader. Easy enough. But how do we elect a leader? All machines must agree on who the leader is—leader election requires reaching consensus, and must have safety and liveness properties.

In Raft, machines can try to become the new leader by starting an election. Doing so changes their role to candidate. Leaders are appointed until they fail, and followers only start an election if they believe the current leader to have failed. A new leader is elected if a candidate receives the majority of votes. With one exception, which we discuss in the section on safety below, followers always vote in favor of the candidate.

Raft uses terms to guarantee that voting is only done for the current election, even when messages can be delayed. The term is a counter shared between all machines. It is incremented with each election. A machine can only vote once for every term. If the election completes without selecting a new leader, the next candidate increments the term number and starts a new election. This gives machines a new vote, guaranteeing liveness. It also allows distinguishing old from new votes by looking at the term number, guaranteeing safety.

An election is more likely to succeed if there are fewer concurrent candidates. To this end, candidates wait a random amount of time after a failed election before trying again.

 

Log replication: In Raft, users only submit new entries to the leader, and log entries only move from the leader to the followers. Users that contact a follower are redirected to the leader.

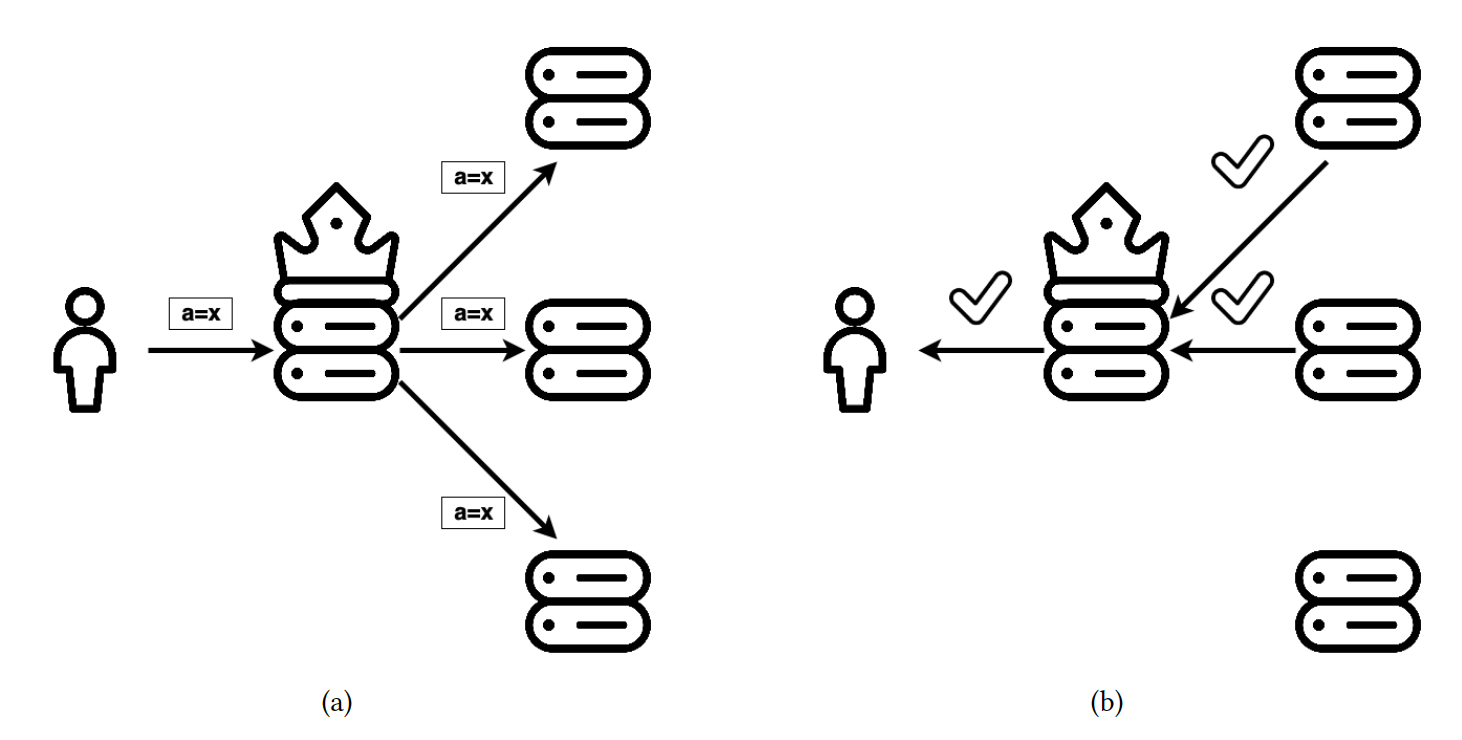
Figure 4. Log replication in Raft. The crown marks the leader.

New entries are decided, or “chosen,” once they are accepted by a majority of machines. As Figure 4 illustrates, this happens in a single round-trip: (a) The leader propagates the entries to the followers and, (b) counts the votes and accepts the entry only if a majority in the system voted positively.

Log replication is relatively simple because it uses a leader. Having a leader means, for example, that there cannot be multiple log entries contending for the same place in the log.

 

Safety in Raft: Electing a leader and then replicating new entries is not enough to guarantee safety. For example, it is possible that a follower misses one or multiple log entries from the leader, the leader fails, the follower becomes a candidate and becomes the new leader, and finally overwrites these missed log entries. (Sequences of events that can cause problems are a staple of consensus-protocol analysis.) Raft solves this problem by setting restrictions on which machines may be elected leader. Specifically, machines vote “yes” for a candidate only if that candidate’s log is at least as up-to-date as theirs. This means two things must hold:

1. The candidate’s term must be at least as high as the follower’s, and
2. The candidate’s log entry index must be at least as high as the follower’s.

When machines vote according to these rules, it cannot occur that an elected leader overwrites chosen (voted upon) log entries. It turns out this is sufficient to guarantee safety; additional information can be found in the original article.

 

 

References:

[1] Diego Ongaro, John K. Ousterhout (2014) In Search of an Understandable Consensus Algorithm. USENIX Annual Technical Conference.