We just saw that time-reversal symmetry can forbid the topological invariant to take a certain set of values. We now study another case where a symmetry changes the topological properties dramatically.

Let’s now take a system where we can split all the degrees of freedom into two groups (say group AA and group BB) such that the Hamiltonian only has nonzero matrix elements between two groups, and not inside each group. This situation arises naturally when the lattice has two sublattices, as in the hexagonal carbon lattice of graphene. So let’s imagine our quantum dot is now a graphene dot:

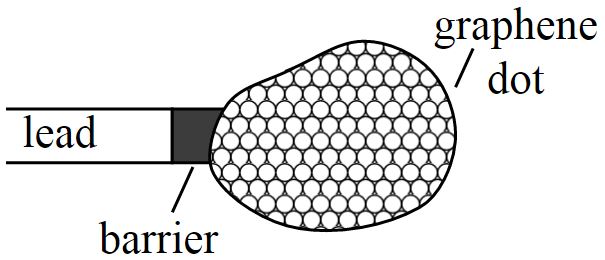
As a consequence of sublattice symmetry, the Hamiltonian of the graphene dot looks like this:

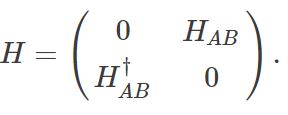
We can once again generate a random Hamiltonian with sublattice symmetry, here:

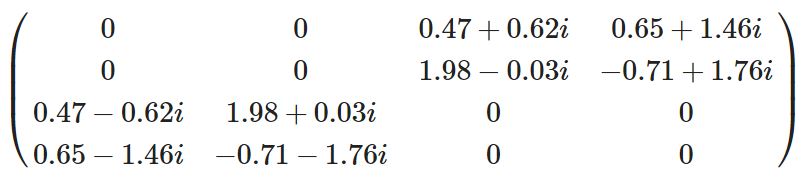
If we introduce a diagonal matrix σzσz that equals +1+1 for sites on sublattice AA, and −1−1 for sites on sublattice BB, we can write the sublattice symmetry of the Hamiltonian as

This immediately means that if (ψA,ψB)T(ψA,ψB)T is an eigenvector of the Hamiltonian with energy εε, then (ψA,−ψB)T(ψA,−ψB)T is an eigenvector with energy −ε−ε. A symmetric spectrum is the consequence of sublattice symmetry.

What does this mean for the topological classification? Clearly, the number of states with negative energy is the same as the number of states with positive energy, and that means we don’t ever expect a single level to cross zero energy.

Let’s once again see if this is correct by transforming a random Hamiltonian with sublattice symmetry into another one.

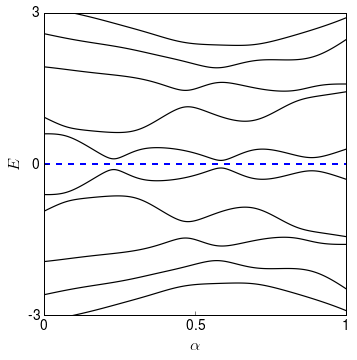
Indeed, we can deform all the Hamiltonians with sublattice symmetry into one another without closing the gap. This means that an extra symmetry may render topological classification trivial.

Question