FERMION OPERATORS AND MAJORANA OPERATORS

Let’s start from the creation and annihilation operators c†c† and cc of a fermionic mode. These operators satisfy the anticommutation relation c†c+cc†=1 and, furthermore, square to zero, c2=0 and (c†)2=0 They connect two states |0⟩ and |1⟩ which correspond to the ‘vacuum’ state with no particle and the ‘excited’ state with one particle, according to the following rules c|0⟩=0, c†|0⟩=|1⟩ and c†|1⟩=0.

When you have a pair of  and c† operators, you can write them down in the following way

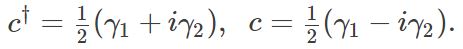
The operators γ1 and γ2 are known as Majorana operators. By inverting the transformation above, you can see that γ1=γ1† and γ2=γ2†. Because of this property, we cannot think of a single Majorana mode as being ’empty’ or ‘filled’, as we can do for a normal fermionic mode. This makes Majorana modes special.

You can also check that to maintain all the properties of  and c†, the operators γ1 and γ2 must satisfy the following relations:

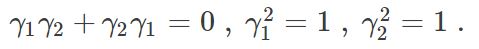
You can see that Majorana modes are similar to normal fermions in the sense that they have operators which all anticommute with each other. Using Majorana modes instead of normal fermionic modes is very similar to writing down two real numbers in place of a complex number. Indeed, every fermion operator can always be expressed in terms of a pair of Majorana operators. This also means that Majorana modes always come in even numbers.

The two Majorana operators γ1,γ2 still act on the same states |0⟩ and |1⟩. If these two states have an energy difference ϵϵ, this corresponds to a Hamiltonian H=ϵc†c. We can also express this Hamiltonian in terms of Majoranas as H=12ϵ(1−iγ1γ2).

But is it possible to have a single isolated Majorana mode, one that is not close to its partner? The naive answer is ‘no’: condensed matter systems are made out of electrons, and these always correspond to pairs of Majoranas. However, it turns out that by engineering the Hamiltonian in a special way it actually is possible to separate two Majoranas.

UNPAIRED MAJORANA MODES IN A MODEL OF DOMINOES

Let’s see how creating isolated Majoranas can be done. Let us consider a chain of  sites, where each site can host a fermion with creation operator cn†. Equivalently, each site hosts two Majorana modes γ2n−1 and γ2n. This situation is illustrated below for N=4, where each site is represented by a domino tile.

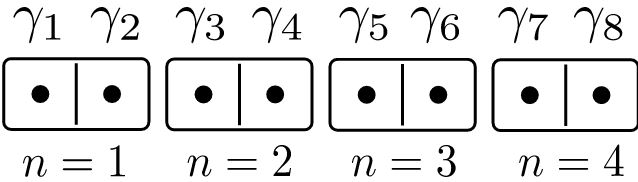
What happens if we pair the Majoranas? This means that the energy cost for each fermion to be occupied is μ, and the Hamiltonian becomes

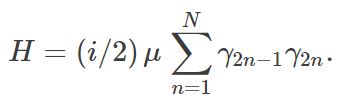
This is how the pairing looks:

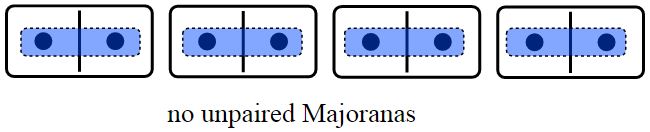
All the excitations in this system have an energy ±|μ|/2, and the chain has a gapped bulk and no zero energy edge states.

Of course this didn’t help us to achieve our aim, so let’s pair the Majoranas differently. We want only one Majorana to remain at an edge, so let’s pair up the Majoranas from adjacent sites, leaving the first one and the last one without a neighboring partner:

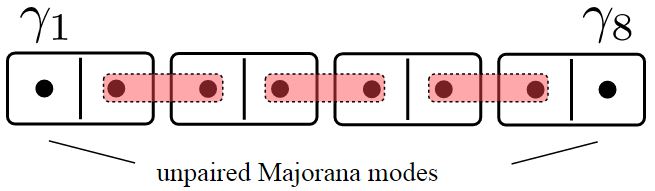
To every pair formed in this way, we assign an energy difference 2t between the empty and filled state, hence arriving at the Hamiltonian

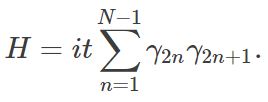
You can see that the two end Majorana modes γ1 and γ2N do not appear in H at all. Hence our chain has two zero-energy states, localized at its ends. All the states which are not at the ends of the chain have an energy of ±|t|, independently on the length of the chain. Hence, we have a one-dimensional system with a gapped bulk and zero energy states at the edges.

THE KITAEV CHAIN MODEL

Let us now try to write the Hamiltonian H, which we have so far written in terms of Majoranas, in terms of regular fermions by substituting γ2n−1=(c†n+cn) and γ2n=−i(c†n−cn) We find that both pairings sketched above are extreme limits of one tight-binding Hamiltonian for a one-dimensional superconducting wire:

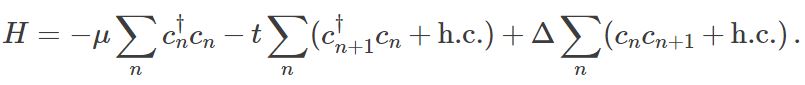
It has three real parameters: the onsite energy μμ, the hopping t between different sites, and the superconducting pairing Δ. Note that the Δ terms create or annihilate pairs of particles at neighboring sites.

Starting from this Hamiltonian, the unpaired Majorana regime is the special point Δ=t and μ=0, while the completely trivial regime of isolated fermions is Δ=t=0 and μ≠0.

As we learned just before, it is useful to write down the above superconducting Hamiltonian in the Bogoliubov-de Gennes formalism H=12C†HBdGC, with C a column vector containing all creation and annihilation operators, C=(c1,…,cN,c†1,…,c†N)T. The 2N×2N matrix HBdG can be written in a compact way by using Pauli matrices τ in particle and hole space, and denoting with |n⟩ a column basis vector (0,…,1,0,…)T corresponding to the nn-th site of the chain. In this way, we have for instance that C†τz|n⟩⟨n|C=2c†ncn. The Bogoliubov-de Gennes Hamiltonian is then given by

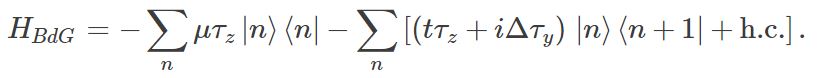
The BdG Hamiltonian acts on a set of basis states |n⟩|τ⟩, with τ=±1 corresponding to electron and hole states respectively. It has particle-hole symmetry, PHBdGP−1=−HBdG with P=τxK.

TOPOLOGICAL PROTECTION OF EDGE MAJORANA MODES

The fact that the Kitaev model can have unpaired Majorana zero modes is certainly interesting. At this point you might however object:

“Unpaired Majoranas appear because you chose one particular, and perhaps even unreachable, set of parameters! Clearly by setting μ=0 you have cut the first and last Majorana mode from the rest of the chain. I bet that if you change the value of μ only slightly from zero, the zero modes will be coupled to the rest of the chain and quickly disappear. So these Majorana modes may just be an artefact appearing in this highly tuned model!”

Well, let’s test if this objection is true. Let’s start from the situation with unpaired Majorana modes (Δ=t,μ=0) and then increase μ. Then let’s plot the energy spectrum of a chain with N=25 sites as a function of μ, and also keep track how do the two lowest energy states of our system look like, when we change μ (move the slider):

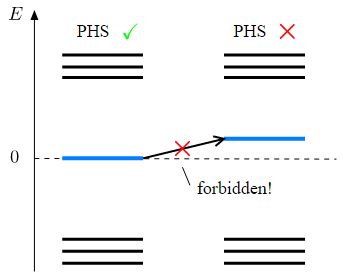
The only possibility to move the energy levels from zero is to couple the two unpaired Majorana modes to each other. However, because of the spatial separation between Majoranas and of the presence of an energy gap, this coupling is impossible. The only way to split the Majorana modes in energy is to first close the bulk energy gap, and that is exactly what happens at large values of μ (to be precise, it happens at μ=2t).

So we have just learned the following:

As you see, our conclusion sounds a lot like what we learned about topology just before. We have come to these conclusions by studying a Kitaev chain on an open geometry with boundaries, and by focusing on the presence or absence of edge states localized at the boundaries of the chain. In the rest of the unit we will see that the presence or absence of edge states can be deduced by studying the bulk alone. In order to do this, we will now study an infinite Kitaev chain without boundaries.

Question