In this worked example we will show that the general solution $x\left(t\right)=A\cdot \sin \left(\omega t+\varphi \right)$ for a mass spring system is a solution to the differential equation that follows from the force balance, which is given by:

This solution is also referred to as the equation of motion of a harmonic oscillator.

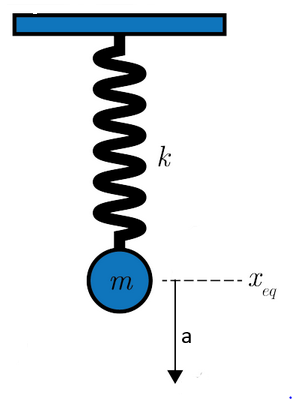
In the equation of motion:

•  $x$ is the position of the mass with respect to the equilibrium position.
• $A$ is the amplitude of the sinusoid, which is the maximum deviation from the equilibrium position.
• $\omega$ is the angular frequency at which the mass oscillates.
• $\varphi$ is the phase deviation, which causes a nonzero starting point.

This worked example provides a framework to show that the equation of motion presented above is indeed a solution to the differential equation for the harmonic oscillator and to determine under which condition this is true.

In this exercise, you can write $\omega$ as omega and $\varphi$ as phi.