4.1 Fourier’s law: examples
Course subject(s)
4. First step into heat and mass transfer
EXAMPLE 4.1A: HEAT CONDUCTION THROUGH A MUG WALL (MEDIUM)
If you drink coffee or tea, heat is lost to the surroundings by means of conduction through the wall of your mug. To simplify the example, we will assume that the energy loss is constant.
The question is: can we calculate the energy loss Φq?
What do we know? Our mug has a height of 10 cm and is completely filled with coffee of 80oC. The inner diameter is 6 cm and the outer is 6.5 cm. Assume that the heat conductivity coefficient λ = 1 W/(m·K) and that the room temperature is 20oC.
Sorry but there don't seem to be any downloads..
Subtitles (captions) in other languages than provided can be viewed at YouTube. Select your language in the CC-button of YouTube.
EXAMPLE 4.1B: LIVING IN AN IGLOO (MEDIUM)
Heat transfer, via conduction, plays an important role in daily life. This is especially true for the Inuits, who find shelter in their snow built Igloos that protect them from the low outside temperature. In this exercise, we will consider a half spherical igloo of radius R = 2m. The wall of the igloo consists of 30cm of thickly compressed snow blocks. The heat conductivity of the compressed snow is 0.3 W/mK.
If the outside temperature is -20oC and the inside needs to be at +20oC: how many humans need to be inside the igloo to achieve this with only the heat produced by the humans?
We will use the following data and assumptions:
– the situation is steady state
– heat is only lost through the wall of the igloo (so we ignore the floor)
– the only resistance against the heat flow is in the walls of the igloo
– a human produces about 150 Watt
- In a steady state, what is the relation between the heat flow through the wall and the temperature difference accross the wall?
- Set up a heat balance for the igloo.
- Compute how many people are roughly needed for the situation sketched above.
Sorry but there don't seem to be any downloads..
Subtitles (captions) in other languages than provided can be viewed at YouTube. Select your language in the CC-button of YouTube.
EXAMPLE 4.1C: CONDUCTION IN A ROD WITH INTERNAL HEAT PRODUCTION (ADVANCED)
In this exercise, we are going to analyse the temperature distribution in a straight rod in which heat is produced internally. The rod has a length L and a constant cross sectional area A. You may think of it as a cylinder. Both ends of the rod are kept at a fixed temperature T0. Inside the rod, heat is produced. This heat production is uniform, i.e. in every part of the rod the same amount of heat per unit volume is produced. We will denote this by Q”’ (in J/m3s). The conductivity of the material, λ, is constant.
We are going to analyze a steady state and we may use the fact that the rod (apart from its ends) is ideally insulated. This means that we can treat the problem as 1-dimensional, with the only relevant coordinate, the x-coordinate which runs parallel to the rod.
- Draw a sketch of the situation and concentrate on the heat flows and production of a small part of the rod, between x, x+dx.
- Set up a steady state heat balance for this small part dx.
- Show that the temperature distribution of the rod is governed by the following differential equation:
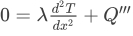
- Provide the necessary boundary conditions to solve this problem.
- Solve the temperature equation and show that, as expected, the temperature at the middle of the rod is the highest.
Sorry but there don't seem to be any downloads..
Subtitles (captions) in other languages than provided can be viewed at YouTube. Select your language in the CC-button of YouTube.

The Basics of transport phenomena by TU Delft OpenCourseWare is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
Based on a work at https://ocw.tudelft.nl/courses/basics-transport-phenomena/.



