5.1 Heat transfer coefficient: examples
Course subject(s)
5 Newton’s law of cooling
EXAMPLE 5.1A: HEATED PLATE (ELEMENTARY)
Inside a horizontal, large, flat plate (area A, thickness d), heat is produced. This is done in a uniform way and thus the heat production per unit volume and per second, Q‴, is constant. The flat plate cools down via the top and bottom area. The heat transfer coefficient for both sides is h. The temperature of the surrounding air is: T∞. The resistance to heat flow is located completely outside the plate.
- What can you conclude about the temperature distribution of the plate?
- Derive an expression for the steady state temperature of the plate.
Sorry but there don't seem to be any downloads..
Subtitles (captions) in other languages than provided can be viewed at YouTube. Select your language in the CC-button of YouTube.
EXAMPLE 5.1B: WATER IN THE CENTRAL HEATING (MEDIUM)
Water in central heating systems has a temperature of about 60oC. It flows through our building in copper tubes. In this exercise, we will be concerned with the unwanted cooling down of this water in the tubes, rather then in the radiators of the heating system.
Suppose that water is flowing through a copper tube (wall thickness 2mm, length 2m, inner diameter 2cm, heat conductivity
![]()
The inlet temperature is 60oC, the outlet temperature unknown. The flow rate through the tube is
![]()
The temperature of the surroundings is 20oC.
- If all resistance to heat would be in the tube wall, show that the water would cool down substantially. An order of magnitude estimate is sufficient.
- The external heat transfer coefficient is about
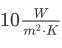
Show that the water only marginally cools down. Again, an estimate is sufficient.
Treat this problem as steady state and approximate the tube wall as a flat plate when calculating the heat transfer.
Sorry but there don't seem to be any downloads..
Subtitles (captions) in other languages than provided can be viewed at YouTube. Select your language in the CC-button of YouTube.
EXAMPLE 5.1C: COOLING SPHERE (ADVANCED)
We will investigate the cooling of a sphere that is surrounded by a cold gas or liquid. We take the case that the resistance to heat is completely outside the sphere. Consequently, the temperature distribution inside the sphere is uniform, i.e. it does not depend on the position in the sphere. Of course, the temperature is still a function of temperature, as the sphere is cooling down.
Furthermore, we will assume that the transport mechanism for heat in the surrounding liquid or gas is conduction only. During the lectures, we have set up a heat balance (as a special form of energy balance) for the sphere, that describes the change of the temperature of the sphere with time. It reads as:
![]()
can write
![]()
and for this case we know Nu is a constant, i.e. Nu=2.
Question: can you solve the differential equation and find the temperature of the sphere as a function of time?
Sorry but there don't seem to be any downloads..
Subtitles (captions) in other languages than provided can be viewed at YouTube. Select your language in the CC-button of YouTube.
BONUS: EXAMPLE 5.1D: HOT ROAD (ADVANCED)
Imagine you are on a black, asphalt road somewhere in the tropics. It is a sunny day and the sun is radiating at
![]()
Recent reports, during a heat wave in India, reported that the asphalt was melting. Is that possible?
In order to find out, we are going to analyze the situation. We do the following:
- Set up a heat balance for the road.
- Estimate the temperature of the road.
The surrounding air has a temperature of about 40oC.
Sorry but there don't seem to be any downloads..
Subtitles (captions) in other languages than provided can be viewed at YouTube. Select your language in the CC-button of YouTube.

The Basics of transport phenomena by TU Delft OpenCourseWare is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
Based on a work at https://ocw.tudelft.nl/courses/basics-transport-phenomena/.



