5.2 Analogy between heat and mass transfer: examples
Course subject(s)
5 Newton’s law of cooling
EXAMPLE 5.2A: COOLING OF AN ALUMINIUM PARTICLE IN AIR (ELEMENTARY)
In this example, we will look at an industrial process: making small particles. In this case: alumina particles. Rather than grinding, we will make them from a melt that we spray with a kind of shower head. Thus, we form hot, small droplets of alumina that fall down and they cool down while falling. For simplicity, we assume that the particle is already solidified.
Question: if such a particle falls through air, what height do we need to have the particle cooled down, such that it is cold enough to be packaged?
Data:
Initial particle temperature: T0=80oC
Diameter particle: D=1mm
Temperature air: 20oC
The resistance to heat transfer is outside the particle.
We will split this up into parts. One part being the terminal velocity, as that partly governs the Nu-number. We have seen how to do that in week 3, so we assume here that we did the force balancing and found that the terminal velocity equals 8m/s. For these conditions, the external Nu-number equals: Nu=15.
- Formulate an unsteady heat balance.
- Find an appropriate h-relation.
- Solve the problem and estimate the required height.
Sorry but there don't seem to be any downloads..
Subtitles (captions) in other languages than provided can be viewed at YouTube. Select your language in the CC-button of YouTube.
EXAMPLE 5.2B: EVAPORATING AIR REFRESHENER (MEDIUM)
A spherical air refresher (made of a solid material) is slowly evaporating. The change of its diameter is governed by the following equation:
![]()
It has been derived from a mass balance over the sphere.
We are going to put in numbers here to see how fast the evaporation takes place. Our sphere has an initial diameter of 1cm. We will try to find the evaporation time without looking up exact numbers.
- Without any calculation, what would you estimate for the time needed to halve the diameter (just use your gut feeling)?
- Make an estimate based on estimating the relative quantities.
Sorry but there don't seem to be any downloads..
Subtitles (captions) in other languages than provided can be viewed at YouTube. Select your language in the CC-button of YouTube.
EXAMPLE 5.2C: REMOVING A SALT LAYER – PART 1, THE LIQUID (ADVANCED)
A layer of salt has been formed on the inside of a tube that is normally used to transport water. In order to clean the tube, fresh water is flowing through the tube. The salt is soluble in water and the layer will, thus, gradually disappear.
The salt has a solubility c* = 50 kg/m3, the tube has a diameter D = 2.5cm, the diffusion coefficient of salt in water is 2 10-9. For water, we obviously have: density 1000 kg/m3 and viscosity 1 mPas. The water velocity in the tube is 1 m/s. Finally, we may use the fact that the layer of salt is much thinner than the tube diameter.
In this example, we are going to inspect the solving of the layer in a quasi-steady state. This means that it is not really steady state, as the salt layer is disappearing, but that the the d/dt term in the mass balance is much smaller than any of the other terms. Thus, we can ignore it and set it to zero.
- Is this flow laminar or turbulent?
- Set up a mass balance for a small part out of the tube + salt layer between x+dx. This mass balance should describe the concentration of disolved salt in the water. Assume quasi-steady state.
- Solve this mass balance and find the concentration profile of salt in the water as a function of position along the tube.
Sorry but there don't seem to be any downloads..
Subtitles (captions) in other languages than provided can be viewed at YouTube. Select your language in the CC-button of YouTube.
BONUS: EXAMPLE 5.2 D: REMOVING A SALT LAYER – PART 2, THE LAYER (MEDIUM)
In the previous example, we took a look at the dissolving of salt from a layer into a water flow in a tube. We concentrated on the salt concentration in the cleaning water. We have however, not addressed how the salt layer is now shrinking. In this example, we will do that.
Now, we need to find the thickness of the layer as a function of time. We will do so under the assumption that the salt concentration in the water flow is small compared to c∗, thus c∗ − c ≈ c∗, i.e. the driving force is the same everywhere (and at its maximum).
- Set up a mass balance over a small part of the salt layer, between x and x+dx.
- Solve this equation and find the time required to clean the tube wall
- Compute how much fresh water you need for this, if the initial salt layer has a thickness of 1 mm (density of salt ρs=2⋅103kg/m3 ).
Sorry but there don't seem to be any downloads..
Subtitles (captions) in other languages than provided can be viewed at YouTube. Select your language in the CC-button of YouTube.
BONUS: EXAMPLE 5.2E: SHRINKING SPHERE (ADVANCED)
In one of the previous examples, we discussed a slowly evaporating spherical air refresher. The air refresher was slowly evaporating and we assumed that the flow was quasi-steady via diffusion only. In this example, we will look, in detail, at the solution of the Mass Balance that we have been setting up. The mass balance reads as:
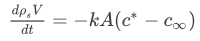
- Find the dependence on the diameter D in the mass balance.
- Solve the equation and show that D does not vary linearly with t.
Sorry but there don't seem to be any downloads..
Subtitles (captions) in other languages than provided can be viewed at YouTube. Select your language in the CC-button of YouTube.

The Basics of transport phenomena by TU Delft OpenCourseWare is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
Based on a work at https://ocw.tudelft.nl/courses/basics-transport-phenomena/.



