Non-linear dynamics
You can explicitly obtain a continuum Lagrangian for the chain which, in the limit \(l(x)\approx\bar{l}\) and \(\bar{\theta}\ll 1\), reads:
\[ \mathcal{L}=\int dx \left[\frac{1}{2}M\left(\frac{\partial u}{\partial t}\right)^2 - \frac{1}{2}K\frac{a^4}{4}\left(\frac{\partial u}{\partial x}\right)^2 -\frac{1}{2}K(\bar u^2-u^2)^2 - \frac{1}{2} K \frac{a^2}{2}(\bar u^2-u^2)\frac{\partial u}{\partial x}\right]. \]
The first term is a linearized kinetic energy, while the second and third terms are the ordinary \(\phi^4\) field theory that you might have encountered for instance while studying the Ising model.
The final term linear in \(\partial_x u\) is topological in the sense that it integrates to the boundary. It ensures that the static kink has zero energy, since the last three terms in the Lagrangian can be combined into a perfect square, that vanishes for the static kink solution (this is sometimes called a BPS state). The topological boundary term does not affect the equations of motions in the bulk, but it breaks the \(\partial_x u \rightarrow -\partial_x u\) symmetry of the \(\phi^4\) theory. That's why the two edges are not equivalent in terms of initiating the kink motion.
The anti-kink solution (with left- and right-leaning states reversed in space) costs a finite stretching energy. Hence, the anti-kink is forbidden in the ground state represented by the linkage limit, where \(k_e \rightarrow \infty\). The anti-kink would require an opposite choice of sign in front of the topological boundary term.
As discussed in the introductory video, however, something that behaves like an anti-kink can be obtained if we stick in the system a rigid bar much longer than the others:
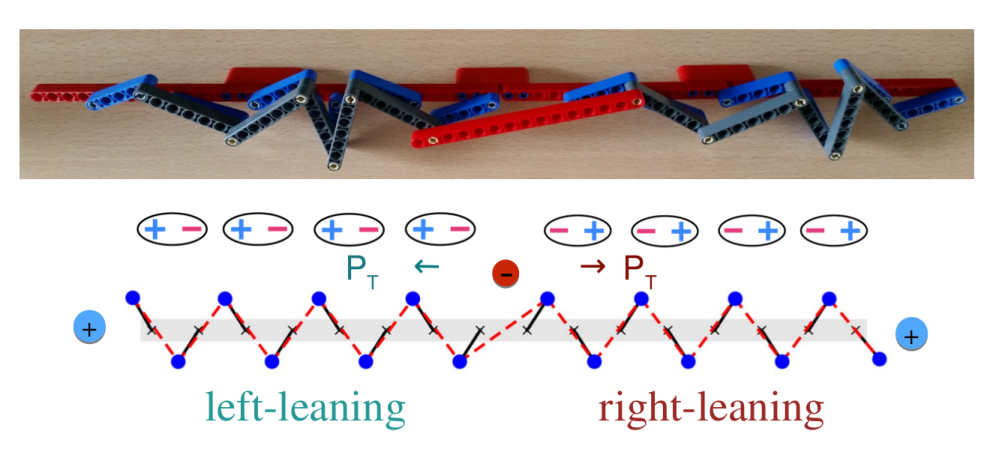
Rather than analyzing mathematically the dynamics of the Lagrangian above, watch the two videos below that show the motion in the linkage limit.
If you are curious about the mathematical details and a systematic study of the dynamics in the springs-rotors system, you can check out the following paper:
Nonlinear conduction via solitons in a topological mechanical insulator
http://arxiv.org/abs/1404.2263
The same reference above contains hints on how to build this structure with LEGO – plus of course all the mathematical details!



