Classically, an expectation value is also called an average, which is simply a weighted sum over possible outcomes where the weights are the probabilities of each outcome.  The expectation value of a random variable X is denoted as

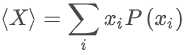
where xᵢ  is a possible outcome, and P(xᵢ) is the probability of observing that outcome. In quantum mechanics, any observable must be represented by a Hermitian matrix, which has real eigenvalues.  As we already have seen, whenever we measure we obtain one of these eigenvalues with some probability, and if we measure many times, we can compute ⟨X⟩ by weighting each possible value of the observable by its estimated probability.  Thus, the “xᵢ” in the above sum is the i-th eigenvalue, and the probability is just given by the “sandwich rule” we saw earlier:

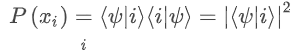
It turns out that there is a result in linear algebra called the spectral theorem, which states that any Hermitian matrix H can be expressed in the following way

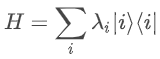
where λᵢ is the i-th eigenvalue of H (a real number) and |i⟩⟨i| is a projector onto the i-th eigenvector of H. We can immediately check whether this makes sense by using the expressions we have already derived

The final expression is indeed the expectation value of the operator H in the state |ψ⟩, which is just an average over every possible result, weighted by however much |ψ⟩ lies in each particular |i⟩ direction.

As an example, if we prepare the state |+⟩ and measure it in the Z basis, each time we will get +1 or -1.  If we do this many times, the weighted average of our results is