Ballooning

On this page, we have some bonus content for you! In this and some subsequent chapters we will treat extra background knowledge for those of you with a particular interest in aviation. This content in completely optional, so if you don’t like this style of content (it will get quite mathematical at times!) or don’t have the time to do it, feel free to click ahead to the next lecture.

Here, we will treat some extra history of ballooning, followed by a mathematical derivation of the equation of state, which will allow us to calculate the lift of a balloon in a more useful way.

History of Ballooning

The twentieth century is often called “the century of flight”. But before the Wright brothers flew their Wright flyer in 1903, mankind had already been flying for 120 years, more than a century, using balloons. For a long time people thought that this was the only way in which humans could fly.

The principle of hot air balloons was already known to the Chinese in the year 300 AD as an invention by Zhuge Liang. The so-called Kong-Ming lanterns were used primarily for military purposes, probably for communication. Today Kong-Ming lanterns are still widely used in Asia at festivals and in many other celebrations. They are also sometimes seen in Europe (and are responsible for numerous UFO reports).

CC BY SA 3.0 Richy on Wikimedia Commons

Surprisingly enough, as far as we know, the Chinese never considered to use a larger version to lift a human. The first ones to seriously consider manned flight with a balloon were two French brothers, Joseph-Michel Montgolfier and Jacques-Etienne Montgolfier. At the end of the year 1782 they started experimenting with larger hot air balloons, as Prof. Hoekstra explained in the lecture.

The first results were impressive. The lift force that could be generated by increasing the volume of the hot air balloons was larger than they had expected. Consider the effect of scale, of magnification on the ratio of volume (gas, lift) and area (balloon surface, hence the weight).

In 1783 the Montgolfier brothers continued their experiments. The first living creatures to lift off in a man-made device were a sheep, a rooster and a duck. This was not a random collection from a nearby farm. It was part of a scientific experiment to explore whether humans would be able to breathe and survive a flight higher in the atmosphere, away from the Earth’s surface. Birds that were able to fly could do this, so the duck was a control sample to see whether the craft itself perhaps had an effect. Whether it was a matter of accommodation or a difference between the physiology of birds and mammals had to be tested by including a rooster, a bird that did not fly, and the sheep, as a mammal functioned as a model human. All animals survived the flight in good health. (Well, the rooster had a broken wing, because it had been kicked by the sheep)

Public Domain, retrieved from Wikimedia Commons

These experimental flights had by now drawn an immense attention of the crowd and the nobility. Even the king, Louis XVI witnessed the balloon flight with the animals. The next step was to have humans on board. For this the king proposed to use prisoners as test subjects. However, there were some noblemen who volunteered to be the first humans to fly. One of them was Pilatre de Rozier, a 26 year old physician, who conducted a series of tethered flight experiments before the first real free flight on 21 November 1783. This first real, because untethered, flight was done together with an army officer, the Marquis d’Arlandes.

Pilatre de Rozier continued as a flight pioneer. He set a record for speed (70 km/hr), altitude (3000m) and distance travelled (52 km) in 1784. In 1785 de Rozier dies when he crashed during an attempt to cross the English Channel. Today, hot air balloons are still called Montgolfieres and the hybrid of a gas and hot air balloon is called a Roziere, after its inventor who used hydrogen for the first time.

Public Domain, retrieved from Wikimedia Commons

Many other pioneering flights and new designs followed. Here you can see an experiment by Guyton de Morveau: a balloon with rudders attached to the craft to control the direction of flight. Why doesn’t this work (And hence don’t we see this today on balloons)?

Ballooning Equation of State

You may have heard of the ideal gas law, the relationship between the number of molecules in a gas and its volume, temperature and pressure:

Where . However, this equation is not in a very useful form for aeronautics: it only applies to one amount of gas (n mole with a volume of V). Both n and V are hard to define if you speak about changes of pressure and temperature in the atmosphere.

We will rewrite the ideal gas law to a different form: the equation of state. The advantage is that it does not have the volume or n in it. By using the air density instead, we can use it to describe any point in a flow or in the atmosphere. With the volume that would be far harder:

Here, we change the definition of , the universal gas constant, to  the specific gas constant. For air,

The derivation of this equation of state is as follows: First, we need to get rid of the volume and number of molecules. We can do this by using the density instead:

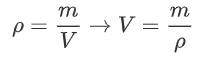
Where we note that we can rewrite n as mass divided by mass per mole:

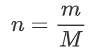
Now we substitute our new expressions for n and V in:

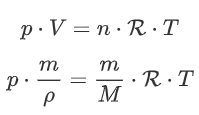
Divide the left and right side by m:

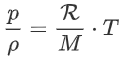
Multiply by ρ:

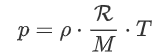
And lastly we define :

As we learned in the lecture, we can calculate the lift of the balloon from the difference of the weight of the balloon and the weight of the air it displaces. You may have also heard this referred to as Archimedes’ Principle:

The lift generated is equal to the weight of the displaced air minus the weight of the gas.

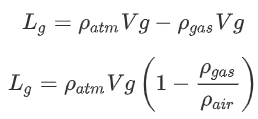
This is true for both gas and hot air balloons, but it is not very practical. Rarely will we know the density of the gas or the hot air. We might know (or be able to model) the density of the atmosphere, which will be explained in module 5.

Lift of Hot Air Balloons

We will begin with a hot air balloon. The interior of the balloon is  hotter than the outside air in the atmosphere. Let us use the above equation with densities as a starting point:

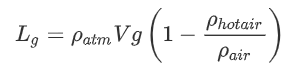
and

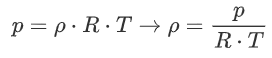
We can then do the following derivation:

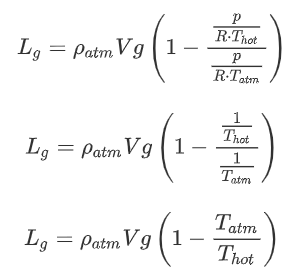
Often, it is more convenient to use , the increase in temperature compared to the outside temperature:

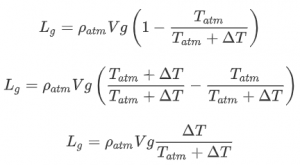
This is an equation that we can use! We know the density and temperature of the atmosphere. When we then need a certain lift we can calculate the required temperature for a given volume of the balloon. Then we can for example see whether that is realistic (temperature should be less than a certain number) or whether we need a bigger balloon.

Lift of Gas Balloons

For gas balloons we use the same equation as a start:

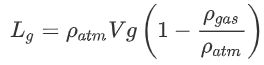
In hot air balloons, the pressure and molar mass were the same inside and outside the balloon. With gas balloons the pressure and temperature are equal. Of course, this is not true in reality: for example the pressure inside the balloon will be slightly higher due to the tension in the balloons material. However, in larger balloons like weather balloons, the balloons are so large that this assumption is valid. Using the assumption of equal pressure and temperature, we can write:

Substituting this in, we get:

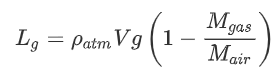
To get a feeling for these numbers, here are the molar masses of some gasses:

• Helium: 4.00 g/mol
• Hydrogen: 2.02 g/mol
• Air (average): 28.97 g/mol

So for helium we find:

If we compare this to hot air balloons:

This implies that  should be six times as high as the atmospheric temperature in Kelvin. So for an outside air temperature of 15 degrees Celsius, this would mean an air temperature approaching 1800 degrees C! That is hotter than a blowtorch! This clearly shows that in terms of generation of lift, Helium is better.

Which reasons can you think of why the majority of balloons use hot air despite this lower efficiency?