Building the mathematical model

In estimation problems, we need a mathematical model to describe the physical situation as good as possible in mathematical terms. The model of observation equations is one way to achieve this goal. It consists of two parts:

1. The functional model, which relates the observations to the unknown parameters of interest. 

2. The stochastic model, which describes the quality of the observations.

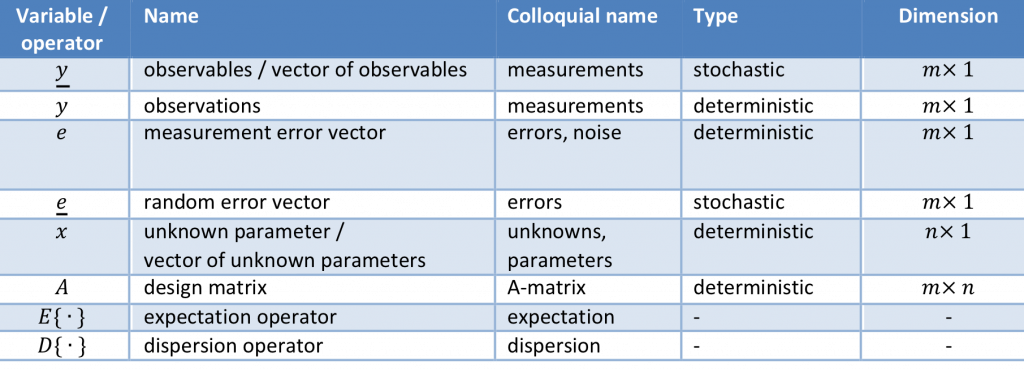
We use a common notation:

• - Lower-case letters, such as \(y\), \(x\), and \(e\), are used to indicate vectors, while upper-case letters such as \(A\) and \(B\) are used for matrices. It should be noted that a scalar is regarded as a \(1\times 1\) vector. Thus, for example the lower-case letter \(x\) can be used to indicate one single number, or a vector of numbers. 


• - Observations, or measurements, are indicated with the letter \( y\). This vector has the dimension \( m\times 1\), where \( m\ge  1\) is the total number of observations. If it is underlined, as in \( \underline{y}\),  it means that the elements are stochastic (or random) variables, which we refer to as observables. If \( y\) is not underlined, the variables are deterministic, and we refer to them as observations.


• - The unknowns, or parameters of interest, are indicated with the letter \( x\) . It has dimension \( n \times 1\), where \( n\ge 1\) is the total number of parameters. It is never underlined, since there is only one true (but unknown) value for (the elements of) \(x\).


• - The functional relation between the observations and the unknown parameters is expressed by the function \(A ()\) (if the functional relation is non-linear) or matrix \(A \) (if the functional relation is linear, or linearized). The matrix \(A\) is also known as the “design matrix”.


• - The errors, or residuals, are indicated with the letter \( e\) . This vector has the same dimension as the dimension of the observations, i.e., \(m \times 1\). If it is underlined, as in \(\underline{e}\), it means that the variables are stochastic (or random). If \(e\) is not underlined it means that the variables are deterministic.

The Expectation operator is used to indicate the expected value of a variable, also called the mean. We write it as \(E \{ \}\). If a stochastic variable \( \underline{y}\) has a probability density function, the expectation is defined as a function of (, i.e. integral over)

The functional model of observation equations can be written in two ways:

\[\underline{y}=Ax+\underline{e}\]

or

\[E\{\underline{y}\}=Ax\]