2.2.7 Consistency for Online Gaming, Virtual Environments, and the Metaverse
Course subject(s)
2: Functional Requirements
Various consistency techniques support online games, virtual environments, and, more recently, various metaverses. Key to these techniques is client tolerance to inconsistencies in the virtual world presented to them. Each game genre has a specific tolerance for the timeliness of updates and how inconsistent the values are. Online games span many genres, from tight, small worlds with few players and turn-based interaction (think chess), to open, large, massively multiplayer online games focusing on role-play and moderate player input (World of Warcraft or Runescape), to mid-scale, real-time online strategy and simulation games where a handful of players command up to tens of thousands of objects (Starcraft), to town-scale, fast-paced, visceral online first-person shooters where tens of players hurl at each other (PUBG or APEX Legends).
Dead Reckoning
One of the earliest consistency techniques in games is the dead reckoning. The technique addresses the key problem that information arriving over the network may be stale by the moment of arrival due to network latency. The main intuition behind this technique is that many values in the game follow a predictable trajectory, so updates to these values over time can largely be predicted. Thus, as a latency-hiding technique, dead reckoning uses a predictive technique, which estimates the next value and, without new information arriving over the network from the other nodes in the distributed system, updates the value to match the prediction.
Although players are not extremely sensitive to accurate updates, and as long as the updated values seem to follow an intuitive trajectory will experience the game as smooth, they are sensitive to jumps in values. Thus, when the locally predicted values and the values arriving over the network diverge, dead reckoning cannot simply replace the local value with the newly arrived; such an approach would lead to value jumps that disturb the players. Instead, dead reckoning interpolates the locally predicted and the newly arrived values, using a convergence technique.
The interplay between the two techniques, the predictive and the convergence, makes dead reckoning an eventually consistent technique, with continuous updates and managed inconsistency.
Advantages: Although using two internal techniques may seem complex, dead reckoning is a simple technique with excellent properties when used in distributed systems. It is also mature, with many decades of practical experience already available.
For many gaming applications, trajectories are bound by limitations on allowed operations, so the numerical inconsistency can be quantified as a function of the staleness of information.
Drawbacks: As a significant drawback, dead reckoning works only for applications where the two techniques, especially the predictive, can work with relatively low overhead.
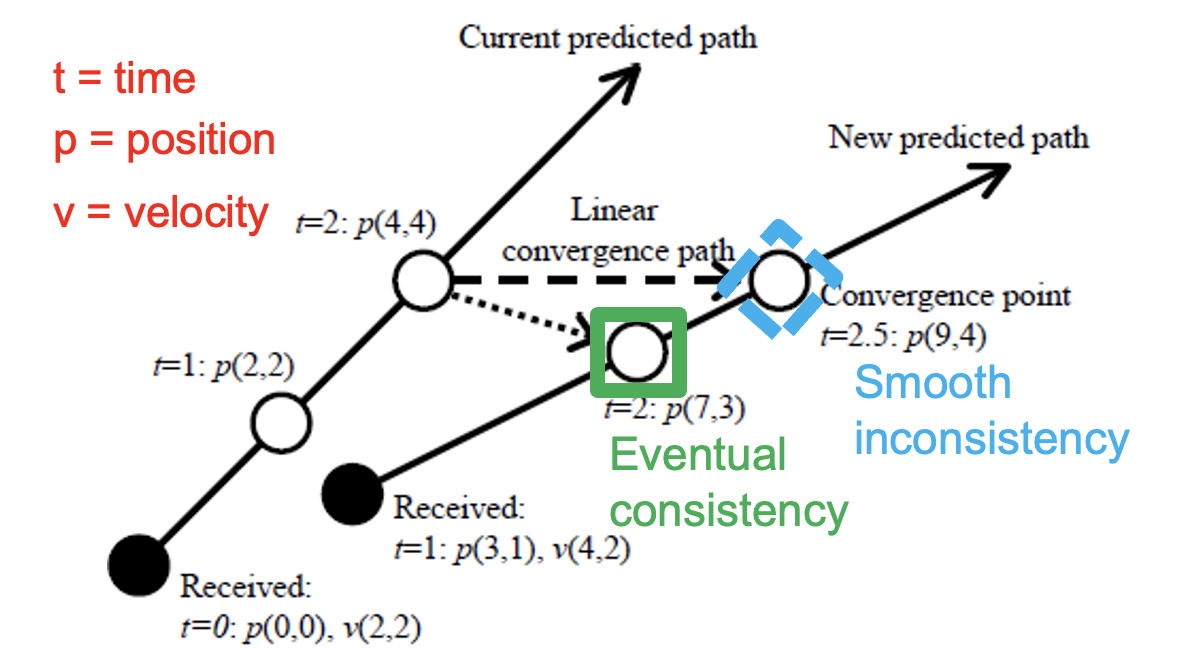
Figure 1. Example of dead reckoning. (Source: [1].)
Example: Figure 1 illustrates how dead reckoning works in practice. In this example, an object is located in a 2D space (so, has two coordinates), in which it moves with physical velocity (so, a 2D velocity vector expressed as a pair). The game engine updates the position of each object after each time tick, so at time t=0, t=1, t=2, etc. In the example, the local game engine receives an update about the object, at t=0; this update positions the object at position (0,0), with velocity (2,2). The dead reckoning predictor can easily predict the next positions the object will take during the next time ticks: (2,2) at t=1, (4,4) at t=2, etc. If the local game engine receives no further updates, this predictor can continue to update the object, indefinitely.
However, the object, controlled remotely, moves differently, and the local game engine receives at t=1 an update that the object is now located at (3,1), with the new velocity (4,2). The game engine has already updated the local value, to (2,2). For the next tick, t=2, the dead reckoning technique must now interpolate the next value (4,4) and the value derived from the received updates (7,3). If it simply replaces the next value with the value derived from the received update, the player will observe a sudden jump, because the next value follows the intuitive path of the previous values the player observed locally, whereas the value derived from the received update does not. Instead, the dead reckoning technique computes interpolated values, which will smoothly converge to the correct value if no new information is received.
If the local game engine keeps receiving new information, dead reckoning ensures a state of smooth inconsistency, which the players experience positively.
References:
[1] Jouni Smed, Timo Kaukoranta, and Harri Hakonen (2002) A review on networking and multiplayer computer games. Turku, Finland: Turku Centre for Computer Science.
Lock-step Consistency
Toward the end of 1997, multiplayer gaming was already commonplace, and games like Age of Empires were launched with much acclaim and sold to millions. The technical conditions were much improved over the humble beginnings of such games, around the 1960s for small-scale online games and through the 1970s for large-scale games with hundreds of concurrent players (for example, in the PLATO metaverse). Players could connect with the main servers through high-speed networks… of 28.8 Kbps, with connections established over dial-up (phone) lines with modems. So, following a true Jevons’ paradox, gaming companies developing real-time strategy games focused on scaling up, from a few tens of units to hundreds, per player. Consequently, the network became a main bottleneck – sending around information about hundreds to thousands of units (location, velocity, direction, status for each other tracked variable), about 20 times per second as required in this game genre at the time, would quickly exceed the limit of about 3,000 bytes per second. To expert designers, these network conditions could support a couple of hundred but not 1,000 units. In a game like Age of Empires, the target limit set by designers was even higher: 1,500 units across 8 players. How to ensure consistency under these circumstances? (Similar situations continue to occur: For each significant advance in the speed of the network and the processing power of the local gaming rig, game developers embark again on new games that quickly exceed the new capabilities.)
One more ingredient is needed to have a game where the state of every unit – location, appearance, activity, etc. – appears consistent across all players: the state needs to be the same at the same moment because players are engaged in a synchronous contest against each other. So, the missing ingredient is a synchronized clock linked to the consistency process.
Lock-step consistency occurs when simulations progress at the same rate and achieve the same status at the end (or start) of each step (time tick).
One approach to achieve lock-step consistency is for all the computers in the distributed system running the game to synchronize their game clocks. Players would input their commands to their local game engines, which the local game engine communicates over the network to all other game engines. Then, every game engine updates the local status based on the received input, either locally or over the network. The game moves in lock-step, and each step consists of the sequence input, communication, then local updates that include input.
A main benefit of this approach is that the approach trades-off communication for local computation: the communication part is reduced only to necessary updates, such as player inputs, and the game engines recompute the state of the game using dead reckoning and the inputs. The network bandwidth is therefore sufficient for a game like Age of Empires with 1,500 moving units.
As a drawback, this approach uses a sequence of three operations, which is prohibitive when the target is to complete all of them in under 50 milliseconds (to enable updates 20 times per second, as described earlier in the section). Suppose performance variability occurs in the distributed system, either in transferring data over the Internet or in computing the updates, for any of the players. In this case, the next step either cannot complete in time or has to wait for the slowest player to complete (lock-step really means the step is locked until everyone completes it).
Another approach pipelines communication and communication processes, that is, updating the state while receiving input from players. To prevent inconsistent results, this approach again uses time ticks, and input received during one step is always enforced two steps later.
Advantages: Such an approach guarantees that performance variability in communicating input between players can be tolerated, as long as it is not longer than twice the step duration (so, 400 ms for the typical tick duration of 200 ms). The tolerance threshold of 400 ms was not chosen lightly and corresponds to the tolerance to latency players exhibit for this game genre, which has been reported by many empirical studies and summarized by meta-studies such as [2]. In other words, for this game genre players still enjoy their in-game experience, even when a latency of 400 ms is added to their input, as long as the results are smooth and consistent.
Disadvantages: As for the first approach, performance variability, which is predominantly caused by the processing of the slowest computer in the distributed game or by the laggiest Internet connection, can cause problems. The problems occur only when the performance variability is extreme, closer to 1,000 ms than to 400 ms over the typical performance at the time.
A third approach improves on the second by allowing turns to have variable lengths and thus match performance variability. This approach works as the second whenever performance becomes stable near normal levels: The turn length stays at 200 ms, with ticks for communication and computation set at 50 ms.
Whenever performance degrades, this approach provides a technique to lengthen the step duration, typically up to 1,000 ms. Beyond this value, empirical studies indicate the game becomes much less enjoyable. Not only the turn lengthens when needed, but also how it is allocated for computation and communication tasks, next to local updates and rendering. This approach allocates, from the total turn duration, more time for computation to accommodate for a slower computer among the players or more time for communication to accommodate for slow Internet connections.
To make decisions on turn duration, and its specific allocation to communication and computation tasks, the system uses a distributed monitoring technique, where each player reports to the leader (the host for the typical Age of Empires deployment, an elected leader for the peer-to-peer deployment), during each turn, the duration of its local computation task and the latency it observed when sending a ping message to each other player. The leader then computes the maximum of the received values for computation and communication tasks, and makes appropriate decisions. A typical situation could occur when the Internet latency increases, for example to 500 ms, with the turn length increasing correspondingly. Another typical situation, of some computation tasks taking longer than usual, for example, 95 ms, would see the turn stay the normal duration, 200 ms, but inside it the computation tick is increased to 100 ms.
Beyond mere lock-step consistency: Lock-step approaches still suffer from a major drawback: when every player has to simulate locally every input, the amount of computation can quickly overwhelm slower computers, especially when game designers intend to scale well beyond 8 players, to possibly tens or hundreds or thousands for real-time strategy games.
Another approach is to reduce the updates per player to only what is necessary, focusing on what interests the player. An example of this approach appears in our past work [3], where we combine two key ideas. First, we partition the virtual world into areas so that the game engine can select only those of interest for each player. Second, the game engine updates areas judiciously. Some areas do not receive updates because no player is interested in them. Areas interesting for only one player are updated on that player’s machine. Each area that is interesting for two or more players is updated with lock-step or communication-only consistency protocols, depending on the computation and communication capabilities of the players interested in the area.
Conclusion: Trading off communication for computation needs is a typical problem for online games, virtual environments, and metaverses. Lock-step consistency provides a solution based on this trade-off, with many desirable properties. Still, lock-step consistency is challenging when the system exhibits unstable behavior, such as performance variability. In production, games must cope with unstable behavior often. Then, monitoring the system carefully while it operates, and conducting careful empirical studies of how the players experience the game under different levels of performance, is essential to addressing the unstable behavior satisfactorily.
References:
[1] Paul Bettner, 1500 Archers on a 28.8: Network Programming in Age of Empires and Beyond, Gamasutra. March 2001. Last accessed: Jan 2022. URL: https://www.gamedeveloper.com/programming/1500-archers-on-a-28-8-network-programming-in-age-of-empires-and-beyond
[2] Mirko Suznjevic, Maja Matijasevic (2013) Player behavior and traffic characterization for MMORPGs: a survey. Multim. Syst. 19(3).
[3] Siqi Shen, Shun-Yun Hu, Alexandru Iosup, Dick H. J. Epema (2015) Area of Simulation: Mechanism and Architecture for Multi-Avatar Virtual Environments. ACM Trans. Multim. Comput. Commun. Appl. 12(1).
Conit-based Consistency
Although lock-step consistency is useful, in games where many changes occur that do not fit local predictors, so for which dead-reckoning and other computationally efficient techniques are difficult to find, it is better when scaling the virtual world to allow for some inconsistency to occur. In particular, games such as Minecraft could benefit from this.
Conits have been designed to support consistency approaches where inconsistency can occur but should be quantified and managed. In the original design by Yu and Vahdat [1], conits quantify three dimensions of inconsistency: (i) Staleness – how old is this update?, (ii) Numerical error- how large is the impact of this update?, and (iii) Order error- how does this update relate to other updates?
Any conit-based consistency protocol uses at least one conit to capture the inconsistency in the system along the three dimensions. Time elapsed and data-changing operations lead to updates to the conit state, typically increasing inconsistency values along one or more dimensions. At runtime, when the limit of inconsistency set by the system operators is exceeded, the system triggers a consistency-enforcing protocol and the conit is reset to (near-)zero inconsistency across all dimensions.
Conits provide a versatile base for consistency approaches. Still, they so far have not been much used in practice for two main reasons: First, not many applications exist that would tolerate significant amounts of inconsistency. Second, setting the thresholds after which consistency must be enforced is error-prone and application-dependent (and client-dependent, as we indicated in the previous section, where empirical studies showed users could tolerate delays of 400-1,000 ms, but not much more).
Conit-based consistency for games: In our recent work [2], we identified online games, and more specifically Minecraft-like games with a largely modifiable virtual world and much interaction focused around this feature, as applications that can tolerate bounded inconsistency and thus use conits. To solve the second issue preventing conit use in practice, we proposed a new approach, based on dynamic conits (dyconits), where a system component can dynamically change the thresholds of different conit dimensions so it can deliver the needed performance (effectively, a trade-off performance-consistency, but more subtle than in the CAP theorem or in the PACELCA framework we introduce at the end of this module).
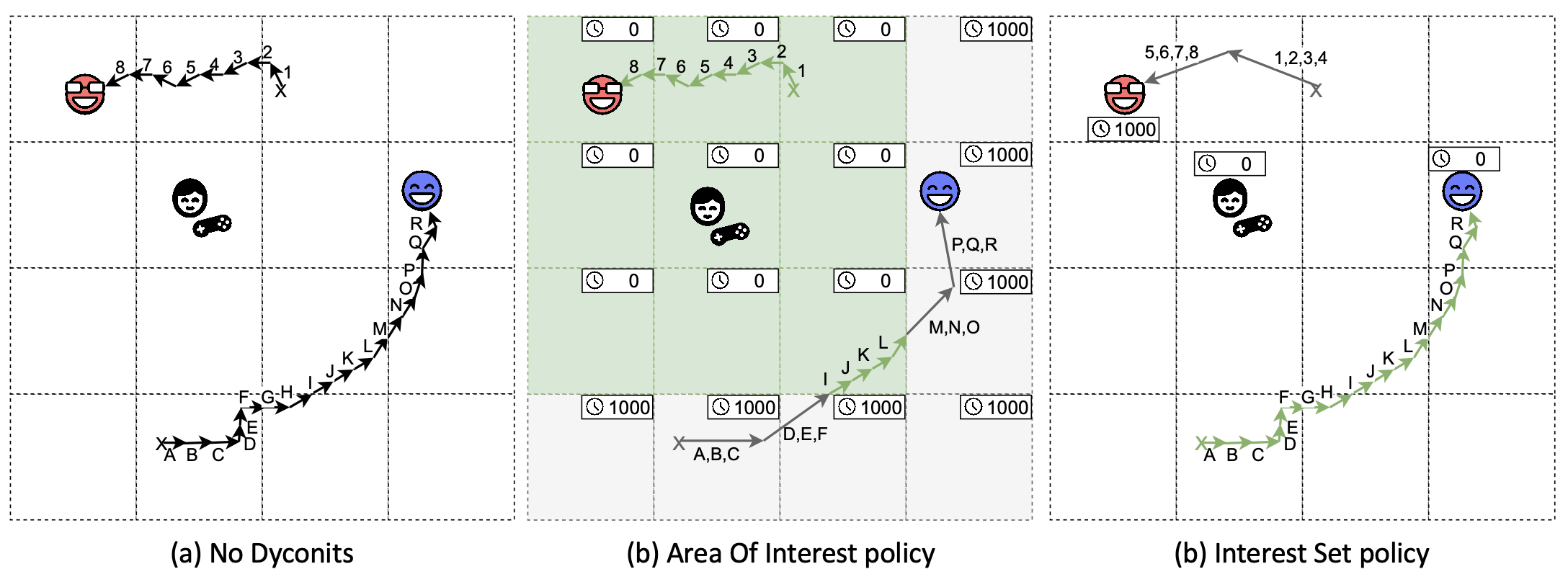
Figure 1. Dyconit policies. (Source: [2].)
Dyconits still require the system to automatically count (increasing) inconsistency. Counting time locally elapsed is trivial for the local game engine. But which operations should count for the conit? We allow different policies to specify the kinds of operations that matter. Figure 1 depicts three such policies; many more are possible. The policies depicted here are: (a) No Dyconits – all messages get transmitted and processed. Note the player (black-and-white figure with a remote nearby) cannot see all the moves of the blue avatar because the game limits the range of sight for all players; (b) Area of Interest — only messages in the AoI of the player (indicated by green the green squares) get frequently transmitted. The inconsistency is bound by the coarsely modeled impact on the game; (c) Interest Set – only the interesting updates (indicated by the green arrows) get frequently transmitted and processed. The inconsistency is bound by the precisely modeled impact on the game.
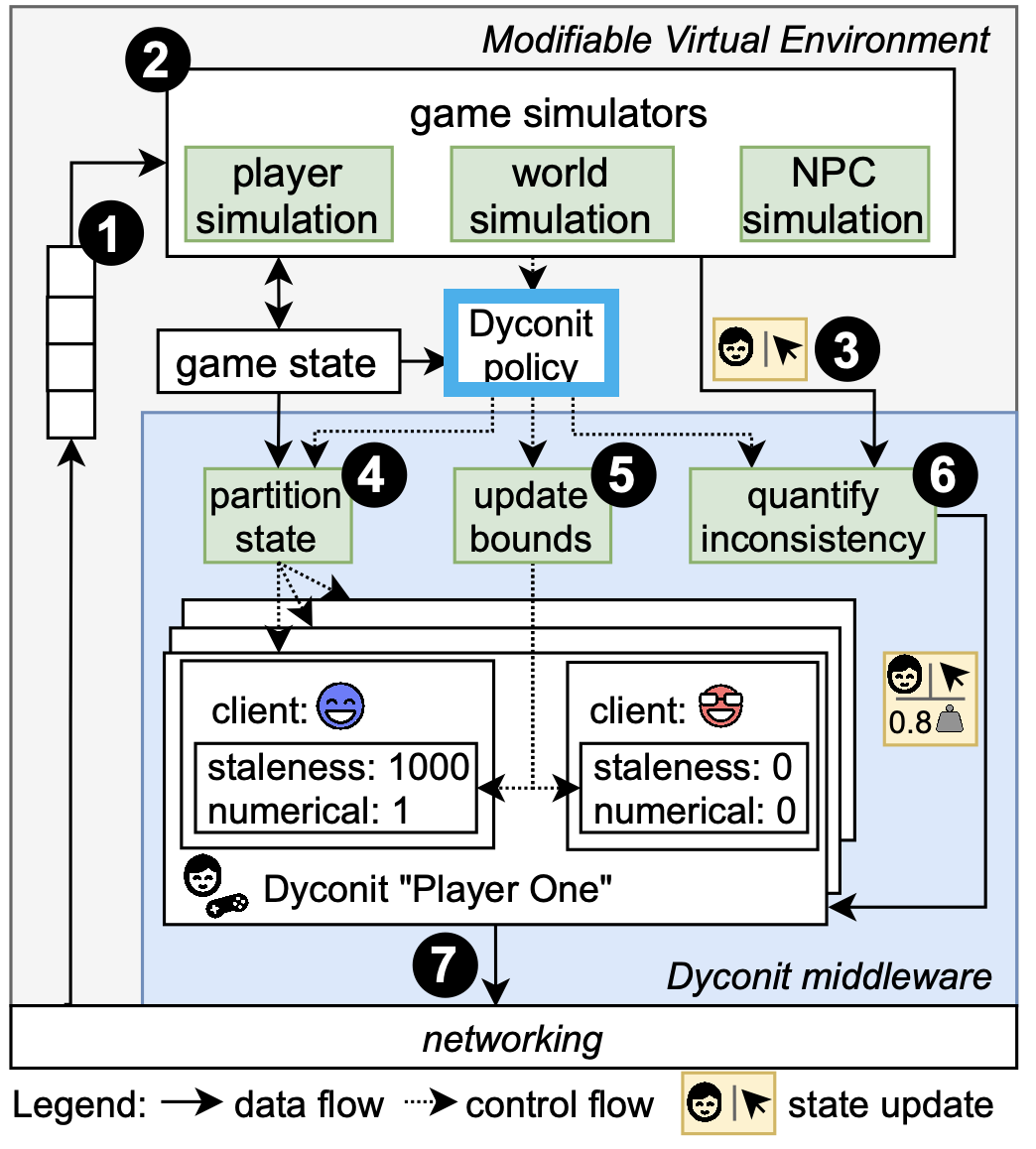
Figure 2. An online, Minecraft-like game using dyconit-based consistency. (Source: [2].)
Merely switching to dyconits is not enough. Instead, a system to manage the dyconits, set their threshold, apply policies for which operations count against the consistency bounds the dyconits define, and enforce the consistency protocols is still needed. Figure 2 depicts such a system and highlights the dyconit management component, based on dyconit policies.
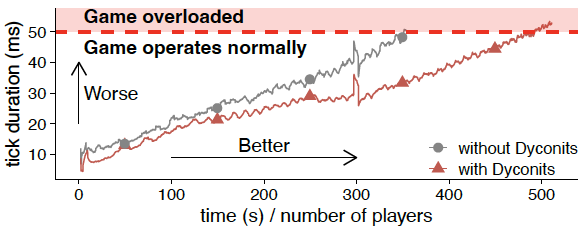
Figure 3. Evidence that in practice, Minecraft-like games work better with dyconits than without. (Source: [2].)
The dyconit system, enforcing dyconit-based consistency using the simple dyconit policies we have just described, works well in practice. Figure 3 shows strong evidence: the Minecraft-like game we have tested extensively, using a peer-reviewed benchmarking suite, performs better when equipped with dyconits than without. In particular, the system with dyconits scales about 40% better.
References:
[1] H. Yu and A. Vahdat (2002) Design and evaluation of a conit-based continuous consistency model for replicated services,” ACM Trans. Comput. Syst. 20(3).
[2] Jesse Donkervliet, Jim Cuijpers, Alexandru Iosup (2021) Dyconits: Scaling Minecraft-like Services through Dynamically Managed Inconsistency. ICDCS 2021.

Modern Distributed Systems by TU Delft OpenCourseWare is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
Based on a work at https://online-learning.tudelft.nl/courses/modern-distributed-systems/



