To recapitulate, the new problem is:

How long does it take for the rainbowfish population to get into its equilibrium state?

Earlier modelling cycles have resulted in the following information:

• P(t) is the number of rainbowfish in the aquarium, with t in days.
• We start with 30 fish. The unbounded birth rate of the fish is b=0.7 per day.
• The death rate is ignored: d≈0.
• The tank can sustain a population of  750 rainbowfish.
• Each day 20 fish are sold.

The resulting initial value problem is:

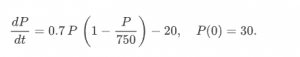
The differential equation has two equilibrium solutions, namely an unstable one of approximately 29.75 and a stable one of approximately 720.25. The second one is relevant for the new problem.

How long does it take to reach that equilibrium? Mathematically, the answer is: “infinitely long” ;-). The nearer P gets to the equilibrium, the lower the value of the derivative (but it stays positive), so the growth will keep slowing down, never reaching zero growth, and P will never reach its equilibrium value.

Luckily, living fish come in units, so we rephrase the question:

How long does it take for the rainbowfish population to reach the last integer before the mathematical equilibrium?

This means that we want to find time teq such that P(teq)=720.

The direction field of P and some possible solutions are shown below.

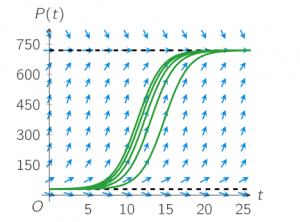
As you can see, many solutions are possible, each of which reaches 720 at a different time. In an exercise of § 2.1 you have estimated the value of teq by imagining one of the solution curves. As you can see, it is rather easy to guess how quickly P rises in the middle. It is much more difficult to guess how long the beginning and the end phase take.

On the following pages, you will learn a method to approximate the solutions in a computer simulation, and then you can estimate much more precisely how long everything will take.