Quality and Types of Errors

Observations or measurements are random or stochastic variables. Notation: \(\underline{y}\).

The quality of the observations is described by the precision and accuracy:

Accuracy: how close the result is to the true value.

Precision: how close repeated measurements are to each other, i.e. how much repeated measurements fluctuate around their mean.

Note: measurements can be precise, but still of low accuracy if the mean of the measurements deviates significantly from the true value.

Precision and accuracy depend on different types of random errors:

Random errors: Stochastic errors, which are the result of (many) unknown and unpredictable sources. On average, the random errors will be zero.
Notation: \(\underline{e}\) 

Systematic bias: Deterministic error which affects all or a subset of the measurements. Systematic biases may result in a constant offset in all measurements, but may also change in time. Systematic biases can be caused for instance due to malfunctioning or wrong usage of the instrument.

Outlier: Deterministic error in one of the measurements, also referred to as blunder or spurious error.

 If we consider the sample mean of a large number of repeated measurements:

\[ \bar{y} = \frac{1}{m} \sum_{i=1}^{m} y_i \]

> the precision of \(\bar{y}\) depends only on the random errors

> the accuracy of \(\bar{y}\) depends on the presence of systematic biases and outliers

Distribution of random errors

In absence of systematic biases and outliers, the individual random errors are the deviations of repeated measurements from their mean:

\[ e_i = y_i -\bar{y}\]

where \(e_i\) is the error in the \(i\)th measurement.

Random errors are usually assumed to have a normal distribution. Since on average the random errors are zero, the expection \(E\{\underline{e}\}=\bar{e}=0\). We thus have:

\[ \underline{e} \sim N(0,\sigma^2_e)\]

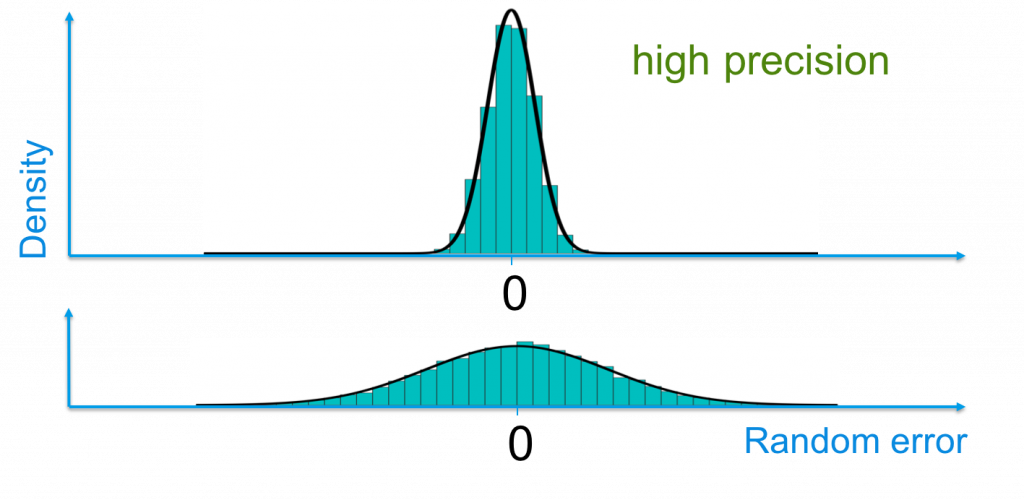
The figure shows an example of an histogram from repeated measurements, as well as the corresponding normal PDF of the random errors for measurements with high precision (top panel) and low precision (bottom panel).