The Jet Equation

Welcome to another piece of bonus content! On this page, we are going to discuss and derive the physical principles of aircraft propulsion in more detail.

As you know by now, the main forces on an aircraft are the lift, drag, weight, and the topic of this lecture: the thrust

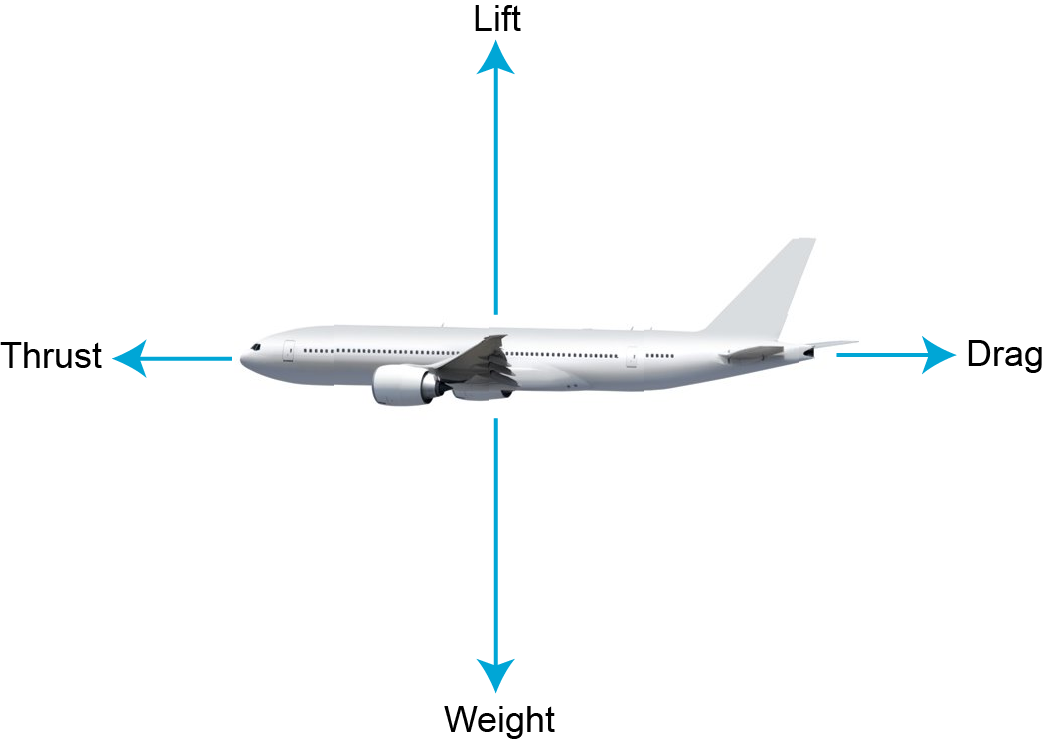
So where does this thrust come from? For a car, or for a bike, the thrust comes from the wheels pushing on the ground; but for an aircraft or a rocket, there’s no ground to push on. Therefore, these engines are what are called reaction propulsion: The engine pushes something else away from itself – air in this case – and the reaction force, as prescribed by Newton’s Third Law of Motion, provides the thrust force. There’s a distinct difference between aircraft engines, which are generally air-breathing engines, and rocket engines, which of course do not have air to take in. Their working is thus different, and the interested reader is encouraged to read up on the Tsiolkovsky rocket equation. In this lecture, we are only focusing on air-breathing engines.

Theory of Air Breathing Engines

The two most common types of aircraft propulsion are the propeller and the jet engine. There are of course a lot of derivative designs. Some of these, like the turbofan, you’ve already encountered. We’ll take a look at some of the more exotic designs at the end of this page. An air breathing engine takes in an amount of air at the front at velocity , and accelerates it to the exit of the engine, where it leaves with . This acceleration provides the thrust:

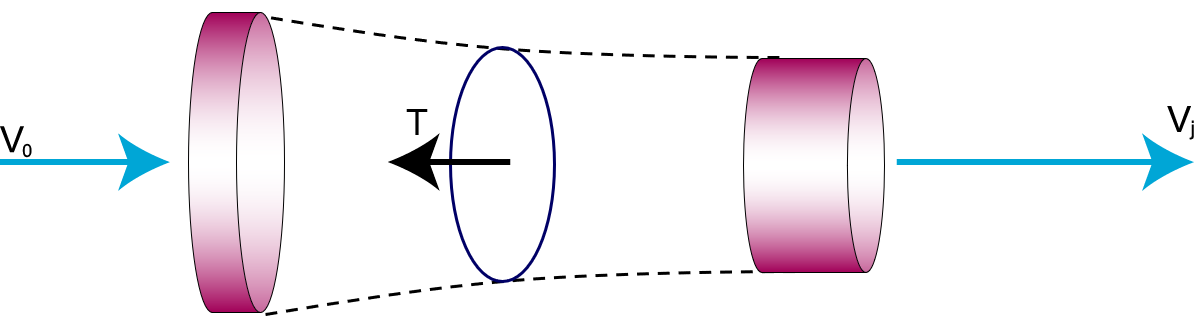
This is the same for both jet and propeller engines; the only difference lies in the fact that a jet engine is a closed “tube”, whereas for a propeller, the tube exists in open air. Regardless, we can express the thrust by looking at the momentum of the system:

Or in other words, the linear momentum of the system is the mass times the velocity. This might not seem immediately useful. However, recall that:

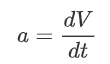
and therefore:

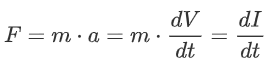
Aha! The force is equal to the change in linear momentum over time! We know the velocity change of the system:

But what is the mass? The engine is in a continuous flow after all. For this, we will use the mass flow : the amount of mass travelling through the engine per second. We can then combine this to say:

Power

With the thrust found, there is another question left for us, important to figure out how much power we need to propel our aircraft (and thus how much power our engine should produce).

Let us consider an aircraft in steady, horizontal flight (not accelerating, and at constant altitude). As the aircraft is flying forward, we can say it travels a distance ΔS  in time Δt, or in other words:

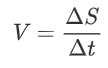
We know from physics that the work W performed by the engine (in Joules) is:

As power is work over time, the available power from thrust is thus given by:

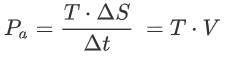
So where does this power come from? An engine produces a certain “Brake power” or “Shaft power” P_br. This is related to the available power through the propulsive efficiency :

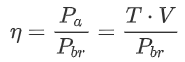
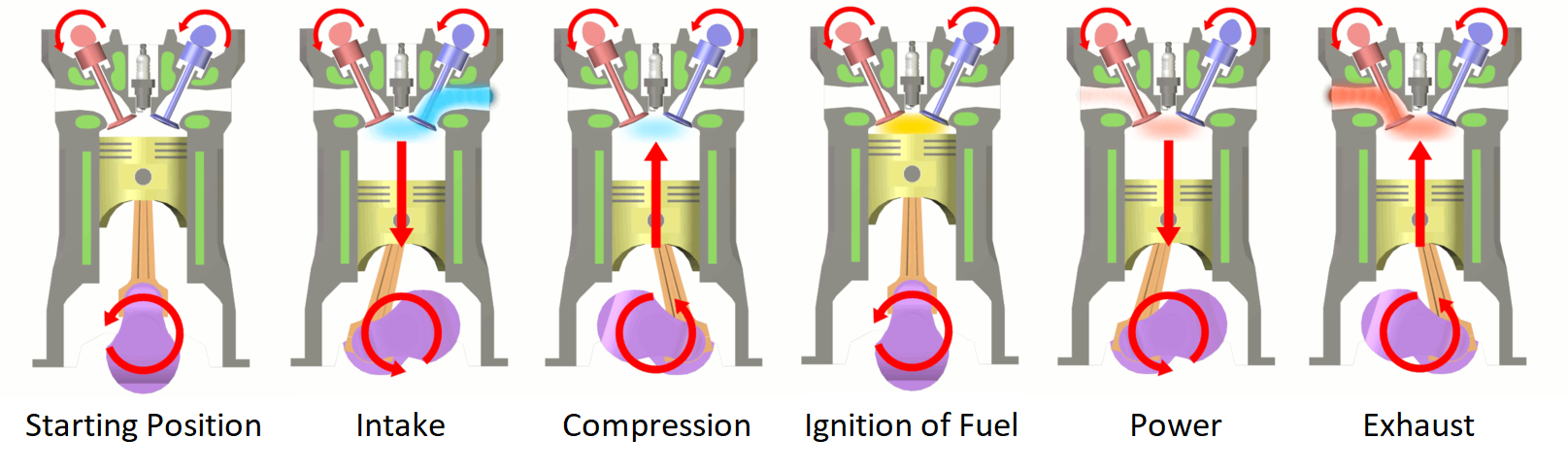
Engines produce this power through a process known as the “Otto cycle”:

CC BY-SA 3.0 Webcaplet on Wikimedia Commons

The engine starts by letting in air from the outside. This air is then compressed. Heat is added to the compressed air (typically by igniting fuel). Then, we can extract power by expanding the hot, compressed air, and lastly, the waste air and heat is rejected into the environment through an exhaust. These 4 stages (inlet, compression, head addition, power extraction) can be found in any combustion engine. Try indicating them in a jet engine:

Image credit: Shutterstock.com

 

 

Jet Efficiency

Lastly, we shall take a more mathematical look at why modern jet engines are so large.

Image credit: Shutterstock.com

As you’ve seen, modern turbofans (or even turboprops) have an extremely large bypass ratio: only a small percentage of the air goes through the core of the engine, the remainder is passed through a large fan at the front. As Prof. Hoekstra explained in the lecture: “it is more efficient to accelerate a lot of air a little, than accelerate a little air a lot.” Let’s examine this mathematically. We’ve already found what the available power is:

This is the power coming from the engine, that is available to the aircraft. The power actually generated by the engine is the jet power: the power going into accelerating the air pushed out of the engine. Thus, we can define the work done by the engine by examining the change in kinetic energy of the jet:

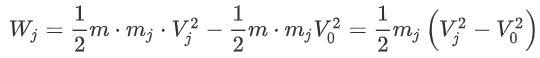
Recall the concept of mass flow. As power is work per time, and mass flow is mass per time, we can simply write:

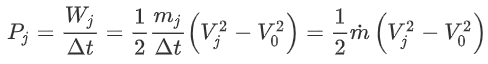
Now, we can simply divide the two to find the jet efficiency:

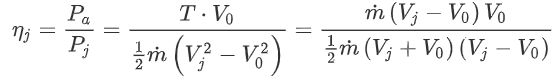
We have  on both sides of the division, so these cancel out:

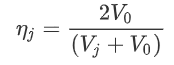
Lastly, we divide both sides of the division by V₀:

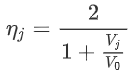
And we’ve found that indeed a lower jet velocity leads to a higher efficiency, regardless of mass flow! Interestingly, you will note we can set the jet efficiency to 100% by simply setting V_j = V₀. Amazing, right? Well indeed, it is possible to have 100% jet efficiency, but that means:

100% efficiency is possible, but only by turning the engine off. Thus, we will always lose some efficiency to the jet. The question of how big to make our engines is thus a big engineering puzzle: on the one hand, a larger engine has a better jet efficiency, but on the other hand, it also has a higher aerodynamic drag, a higher weight (and thus required lift), and a larger engine causes problems when designing the aircraft (as the engine can not touch the ground).