The concept of a topological invariant

In order to know whether there is any path which connects $H$ and $H^{'}$ without closing the gap, we can count the number of levels below zero energy, i.e. the number of filled energy levels. Indeed, for gapped Hamiltonians no energy level can move through zero, but otherwise they can move freely. Therefore continuous transformations exist exactly between Hamiltonians with the same number of energy levels below zero.

Since this number can not change under continuous transformations inside the set of gapped Hamiltonians, we call it a topological invariant $Q$ .

Below, we plot the energy levels along our path from $H$ to $H^{'}$ again, together with our topological invariant, the number of filled energy levels. You can see that this number changes between 3, 4 and 5. Hence we can say that $H$ and $H^{'}$ are not topologically equivalent.

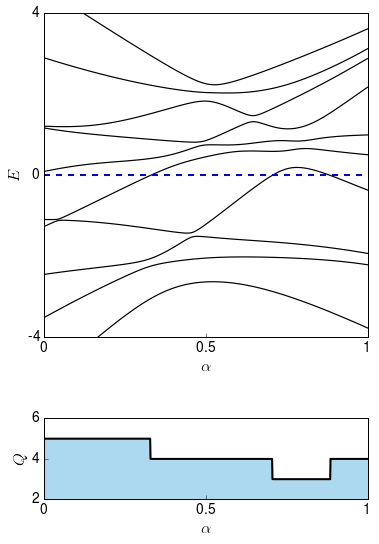
The concept of a topological invariant CC BY SA

The plot makes it clear that we do not actually have to count the number of filled energy levels for both $H$ and $H^{'}$ , so it is enough to keep track of zero energy crossings. Whenever an energy level crosses zero energy, the number of levels below zero energy changes. Such a crossing therefore changes the topological invariant. We call that a topological phase transition.

If two Hamiltonians have a different topological invariant, they must be separated by such a transition. In other words, it is impossible to go from one to the other without closing the gap.

On the other hand, if there are equally many levels crossing from below to above zero energy as the other way around, the number of levels below zero energy does not change. The topological invariant is therefore the same for the initial and final Hamiltonian. In this case, there must be a continuous transformation between the initial and final Hamiltonian which does not close the gap.

Once we have identified a topological invariant, we can classify all quantum Hamiltonians according to its value. In this way we create classes of Hamiltonians which are all topologically equivalent, and we can keep track of all the different topological phases that these Hamiltonians can support.

ROLE OF CONSERVATION LAWS

Let’s now consider the case that the Hamiltonian of the quantum dot satisfies a symmetry constraint. This means that there is a unitary matrix, for example $U = σ_{z} \otimes 1 1$ where $σ_{z}$ is the third Pauli matrix, such that the Hamiltonian commutes with this matrix:

U † H U = H .

This means that the system has a conservation law, and that the Hamiltonian can be brought to a block-diagonal form:

We can now look at the spectrum and the topological invariant of each subblock individually,

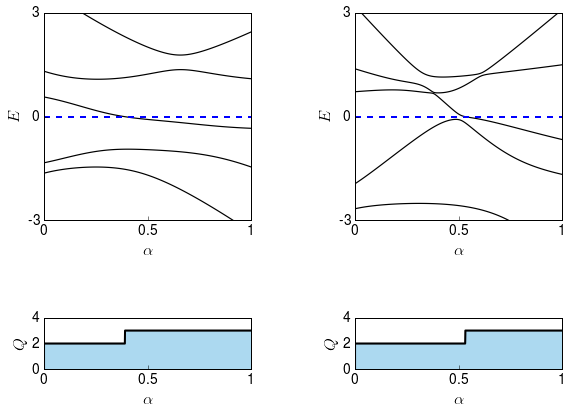
and combine them to get the spectrum and the topological invariant of the whole system:

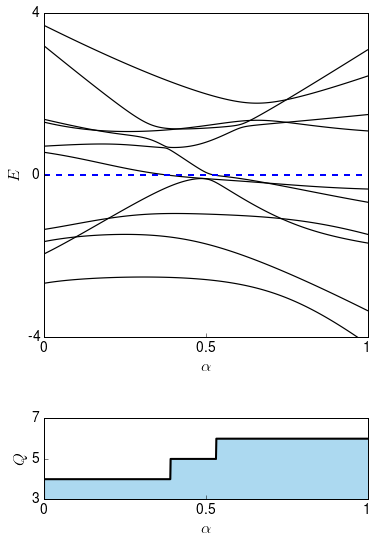
As you can see, unitary symmetries play a rather boring role. As usual, they allow to reduce the dimension of the problem at hand, but nothing more. There are however other symmetries which can have a rich influence on topology. An important example is time-reversal symmetry, as we will see next.