Epidemic model

Model of an epidemic

Simulate the spread of an epidemic, for example of an illness. The basic model describes three populations: a susceptible population, an infected population, and a recovered population. Instead of a disease you could also model the spread of an idea or a rumour.

Epidemic model

The starting model for an epidemic is the so-called SIR model, where S stands for susceptible population, the people that can be infected. I is the already infected population, the people that are contagious, and R stands for the recovered population, people who are not contagious any more.

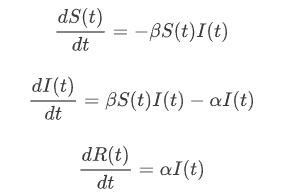
The parameters α and β you will have to choose appropriately.

Simplified epidemic model

In Module 2 (starting from question 7 below) and in Module 3, you use a simplified model: assume that α=0 and that R=0, so once infected, a person stays contagious for ever.

Tasks for the project in Module 2

1. 1. Decide on what disease (or other infectious item) you want to model and in what population.
   2. Collect quantitative information about intial values and about the spread of the disease. If you cannot find enough information, make educated guesses. Do not forget to write down where you found the information!
   3. Can you explain the meaning of the terms of the differential equations in words? What does a high or low value of α mean in words? And β?
   4. Consider the sum of the three populations: S+I+R. Show that in this mathematical model ddt(S+I+R)=0, so the sum is constant. What effects have been neglected in this model?
   5. Choose appropriate units for S, I and R. You can count in individuals, or in millions of people, etc.. Another convenient choice might be to work with fractions of the whole population, so the sum equals 1.
   6. After you have chosen units for S, I and R, derive the units for α and β from the differential equations.
   7. In Modules 2 and 3, start with α=0 and R(t)=0. Because then S+I=C, with C either the total population size, or C=1, you get the relation S=C−I. Substitute this expression into the differential equation for I. Show that this yields a differential equation in I only.
   8. With α=0 and R(t)=0, suppose you have found the solution I(t). How would you then calculate S(t)? Conclusion: for the simplified epidemic model you can just concentrate on the differential equation for I.
   9. With α=0 and R(t)=0, what are the equilibrium points for I? What can you say about their stability?
   10. Now, you can try to find an appropriate value for β, by considering what happens when you start with a small number of infected people. Some of you might have learned the techniques necessary to solve the differential equation for I analytically. Then you could use that analytical solution to find an appropriate value of β for your epidemic. You could also wait until you have programmed the simulations at the end of this module, and choose the value of β then.

Throughout, do communicate well with your teammate, so you make the different choices together. Document every result and decision in your logbook. That will help in the communication between you two, and when you are writing the report later on, you can find all your previous results easily.