Glider model

The trajectory of a glider

A simple model to describe the flight of a glider.

Glider model

The glider flies under an angle θ with the horizon and with (scalar) velocity V. The glider has no engine, and there are three forces working on the glider: gravity, drag and lift. In this simple model, both the drag and the lift are proportional to V2.

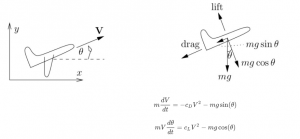
In aerodynamics the socalled angle of attack is the angle between the wings and the oncoming airflow. We assume in this model that there is no wind and that the angle of attack is constant, so parameters cD and cL are assumed to have constant values.

Tasks for the project in Module 2

In this module,  try to get a feeling for this model. The questions below should help you with that.

1. Choose a glider, and collect information about it: its mass, how many passengers besides the pilot, a typical speed. In particular, you want to know its lift-to-drag ratio. On a steady, unperturbed flight, that is the distance travelled by the glider divided by the height lost during that flight. Do not forget to write down where you found the information!
2. You will soon see, that these two differential equations very crudely simplify the complicated aerodynamics of a glider. You might choose just to stay with this model, or you could go somewhat deeper. When you decide to do the latter, first assess what aspects of this model might be too crude. Later in Module 5, you could decide to improve the model.
3. Is angle θ in this model calculated in degrees or in radians? Name the other quantities in the model, and decide on their units.
4. Estimate an approximate value for θ when the glider flies in a long, stable flight.
5. Describe what happens with the plane when θ goes from 0 via π4 to π2. And when θ grows further to 3π4, π, 3π2, 2π?
6. Describe the physical meaning of the terms of the model in words and explain why some are included positively and some negatively. Derive both equations yourself by balancing the forces on the glider. This requires some knowledge of physics.
7. Consider the differential equation for V. What happens with V when the speed is too high? What happens to V when the θ is too negative and aiming too steeply to the ground?
8. Consider the differential equation for θ. What happens to the angle, when the speed becomes too low or the angle becomes too negative?
9. Is there a minimum speed to take off from the ground?

Thoughout, do communicate well with your teammate, so you make the different choices together. Document every result and decision in your logbook. That will help in the communication between you two, and when you are writing the report later on, you can find all your previous results easily.