When performing a quantum algorithm we frequently start with a tensor product of all state at 0, i.e. |0⟩^⊗n state, followed by H^⊗N Hadamard gates for all the qubits.

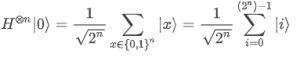
Right after applying the Hadamard gates the state corresponds to

|0⟩+|1⟩+|2⟩+…=|…000⟩+|…001⟩+|…010⟩+…

This procedure allows us to prepare the initial state on a superposition of all possible combinations of 0-1 bit strings encoded in the quantum states. The quantum computer is then able to pursue 2^N “different paths” of possible solutions for the algorithms that are carried out.

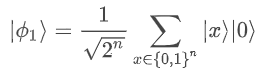
As we can see in the figure the final state corresponds to a superposition of tensor products between the input states |x⟩ and the solutions to a function f,|f(x)⟩. In this case, the function is encoded in the gate U_f.

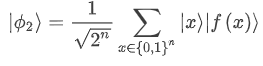
This advantage provided by quantum circuits receives the name of quantum parallelism and it refers to the idea that quantum computers can look for different solutions in “parallel” and “at the same time”. But be careful, parallelism here does not precisely mean that. It is a common misconception to say that quantum parallelism allows different paths to be calculated simultaneously. This is not what happens, but rather the quantum algorithms apply gates to a superposition of quantum states. Each of these individual states can be studied via measurements, after which the wavefunction will collapse to one of the possible paths only.