In classical algorithms we use functions to compute desired quantities. We want to be able to do the same in quantum algorithms. We have seen, however, that quantum circuits rely on a universal set of quantum gates to carry out processes. How can we encode functions in quantum gates?

We start reviewing a set of classical functions known as Boolean functions. These are functions that map from strings of bits of length m to strings of bits of length n.

Two examples are:

• NOT(x) = x XOR 1

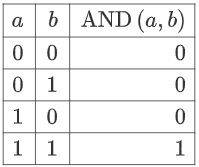
• AND(a,b) = ab mod 2

The quantum counterpart of a classical NOT can be achieved using an X gate. However, the task is not that simple and a bigger set of qubits is usually required.

In general, one can encode Boolean functions into unitaries by increasing the number of qubits to n+m, where n and m correspond to the length of the bits defined above for f. This way a unitary gate U can be defined acting on n+m qubits as:

where

|f(x)+y⟩=|f(x)_n⊕y_n⟩…|f(x)₁⊕y₁⟩

Using this we can encode a counterpart for the AND function!

The reason for this increase in qubits is because unlike classical gates, quantum gates must be unitary. Recall that a unitary gate is any matrix U such that UU^†=I  holds. Importantly, this means that quantum gates are invertible, which intuitively means that we can figure out the input to a function by looking at its output. By contrast, not all classical functions are invertible, because a AND 0 = 0 regardless of whether a = 0 or a = 1. If we want to make a classical function quantum, we first must make it invertible (also known as reversible), and this can easily be done by passing the input along with the output, i.e.

so that we can always deduce the input from the output, because the input is part of the output!