You might have realized that since there are an infinite number of possible gates, that a universal gate set itself could also contain an infinite number of gates. Since this is not very practical, we then ask ourselves, is it possible then to obtain universality from a finite, discrete set?

Incredibly, a set with 3 gates is enough to perform any unitary on n-qubits. This discrete set is composed of the following gates:

• Hadamard 
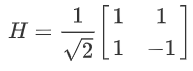
•  T-gate

 

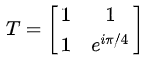
• CNOT

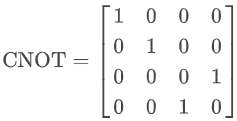
We won’t prove its universality here, but at least it is not terribly complicated to see how any single-qubit gate can be synthesized from just H and T. It turns out that the unitary gate THTH is a rotation about the axis n^ by the angle 2cos−¹(cos²(π/8))≈0.174π, which is an irrational number. We could also work out HTHT, which is a rotation about a different axis m^ by the same angle. The two axes are not collinear, and are

You could (in theory) repeat the gate as many times as needed until θN mod 2π was close enough to the desired angle, for some number of repetitions N. Since the angle θ is irrational, its decimal expansion does not repeat, and thus any desired angle lives somewhere in that expansion. The same argument holds for the other unitary, so we have demonstrated the just having the two gates T and H is enough to rotate by any angle, about two distinct axes, which is enough to reach any point on the Bloch sphere. Of course, the number of gates needed to reach a particular state could be too large to be useful. Furthermore, though we could eventually get close to any desired angle, it would be difficult to systematically reduce the difference between the desired angle and actual one achieved by repeatedly applying one of the two unitaries described above.