Thus far we have seen that quantum states can be changed by applying quantum gates and some of these operations can be reduced to others by clever use gate properties in compiling.

It is interesting to ask ourselves how far we can extend this concept i.e., given a quantum circuit, how much we can reduce it until it boils down to its fundamental components or building blocks.

This concept, called universality, is also present in classical computation and refers to the capability of a set of binary operations to compute any binary function. In the same fashion, we call a set of quantum gates universal if a quantum circuit built out of these gates only, can approximate any unitary operation to arbitrary accuracy.

Multiple sets of quantum gates benefit from universality, for example the set of all two-qubit gates is universal. This is a remarkable result since it implies that when building your quantum computer gates involving a large number of qubits are not required for universal computation!

In particular, one can prove that the set composed of all single qubit operations along with the CNOT gate form a universal set. Take for example a Toffoli gate which can be decomposed in terms of the universal set {CNOT,T,S,H}

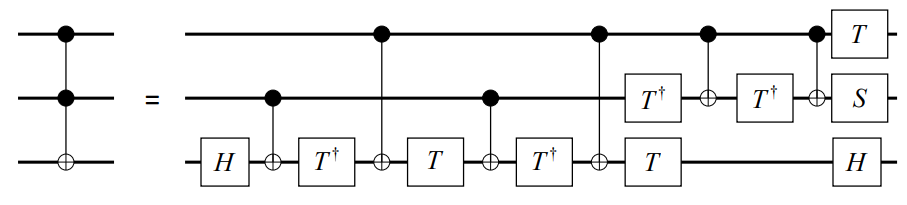
where S  is a π/2 rotation about the Z axis, and T  is a π/4 rotation about the Z axis (so √S=T).

At this point you may wonder why to bother with different universal sets and not simply build a quantum computer with the smallest possible universal set. There are multiple reasons not to do this: first, some gates can be more or less challenging to realize in different architectures. These are gates that naturally result from time-evolution of the quantum state under the Hamiltonian governing the gate-implementation, while other ones need to be engineered carefully.

Secondly, universality states whether a given set can or cannot approximate any unitary but does not give any information about the efficiency of such approximations. There exist unitary transforms which require an exponentially growing number of gates to approximate within some universal sets.

Finally, physical implementation of qubits and qubit gates at the current technological state are prone to errors. It turns out that some gates are more resistant to errors than others. This means that a certain operation might allow for an error on a single qubit to remain isolated in that qubit, while a different gate could propagate that error to other qubits and therefore reduce the performance of the quantum processor. This property is called fault-tolerance but it is outside the scope of this module.