In this subsection, and the following, you will be introduced to the foundational concepts of quantum compiling, which is the art of transforming certain quantum gates into others in often clever ways.  If a quantum computer is a piano, then algorithms are the songs and quantum gates are the notes, and just as two different songs might use different notes, so too do different algorithms use different gates.  It could be that some pianos can play certain notes better than others, so we prefer to use only those notes when playing a song on that piano, and then a song written for one piano would need to be converted to the “preferred” notes of another piano before we could switch instruments.  Or to the dismay of the performer, two consecutive keys might be adjacent on one piano, but completely far apart on another.  We might also ask “bigger” questions, like whether a certain set of notes could be used to play any conceivable song, and if so, how many notes might be needed to do so?  And if not, how close could we get?  These are the kinds of questions thrown around in quantum compiling, and though there are some incredible known results, the field as a whole is quite active, with many open questions waiting to be solved.

In order to reduce the introduction of errors in the system and to compute in shorter times, a quantum circuit is usually reduced to the minimum number of gates possible by using identities between gates. Sometimes the number of gates is not reduced, but a specific set of gates is preferred over another due to the system introducing different errors per gate.

 The process of simplifying a quantum circuit and/or finding a quantum circuit that implements a particular unitary using a specific set of gates is called quantum compiling.

For example, a CNOT gate can be encoded using Hadamards and a CPHASE, and vice versa.

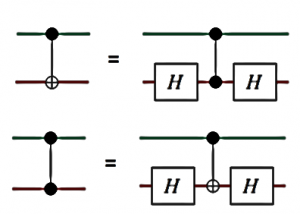
As stated earlier, the process of compiling is strongly dependent on the physical implementation of a quantum computer. This is an extremely important task when scaling up the number of qubits and it becomes very difficult as well.

In fact, quantum compiling is an optimization problem in which a handful of variables are not necessarily fixed. Errors associated with different gates may vary according to temperature, pressure, quality of the system, calibration, among other factors. This means the problem corresponds to an active optimization process, which makes automatization essential and where machine learning is a tool that comes in handy.