Zero-dimensional quantum systems
Imagine a quantum system with a finite number of states N. The Hamiltonian of such a system is represented by a matrix H of dimension N×N. This matrix is Hermitian, H=H†. Its real eigenvalues En correspond to the allowed energies of the system,
H|n⟩=En|n⟩,
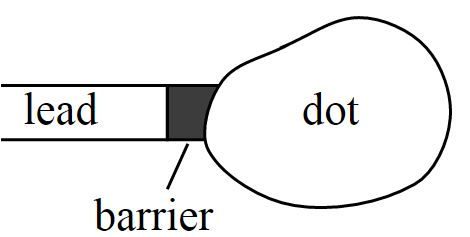
The presence of a metallic lead allows us to measure all the energies E_nEn of the electronic states in the dot with respect to the Fermi level E_FEF of the electrons in the metallic lead. In the following we will set E_F=0EF=0. Hence, all negative energies E_n<0En<0 correspond to filled states in the dot, and all positive energies E_n>0En>0 to empty states. In the sketch, the lead and the dot are separated by a potential barrier, such that they are only coupled very weakly. Thus, we can still consider the dot as an isolated system, to a good approximation.We are now ready to start on the main theme of this course, topology.
TOPOLOGY AND GAPPED QUANTUM SYSTEMS
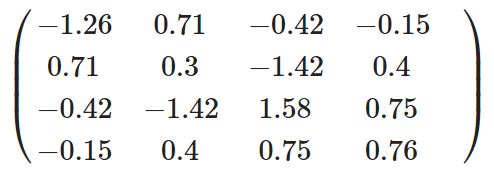
For simplicity, we have taken HH to be real. Let’s now deform this Hamiltonian into another Hamiltonian H′H′, also real. We can imagine that this deformation describes the changes that occur to the dot as an external parameter, such as a gate voltage, is varied. We can parameterize the deformation by
H(α)=αH′+(1−α)H,H(α)=αH′+(1−α)H,
so that at α=0α=0 we are at the initial Hamiltonian and at α=1α=1 we are at the final Hamiltonian. Let’s see what the energy levels do as a function of αα (we use more levels here than in the matrix above so that the spectrum looks more interesting).
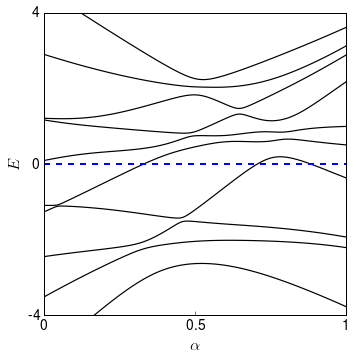
You may notice from the plot that as αα varies, it can happen that an energy level crosses zero energy. When this happens, we break the condition that there should be an energy gap in the system. Notice, however, that this does not necessarily mean that there is no continuous transformation between HH and H′H′ such that the gap does not close. It simply means that this particular path has gap closings. Perhaps it is possible to find another path which does not.
So are HH and H′H′ topologically equivalent or not? Let’s look at this situation:
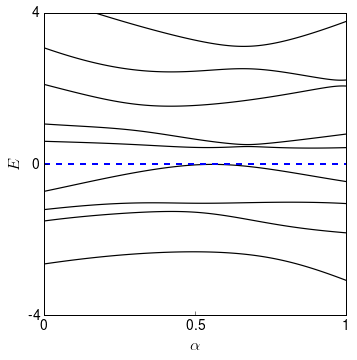
We see that one level does cross zero (even twice), but it seems obvious that we can just push it down a little bit and we find a continuous path between two Hamiltonians. So we need to come up with an easier way to figure out if Hamiltonians can be transformed into each other or not.



