1.2.2 Lecture Notes: Sizing of the EV power train
Course subject(s)
Module 1. How does an EV work?
Rolling resistance force
The rolling resistance force occurs due to the friction between the tires and the driving surface. The rolling resistance force is zero at standstill. When the vehicle starts moving, the rolling resistance force acts in the direction opposite to the direction of motion and can be calculated by the rolling resistance coefficient Cr multiplied by the normal force between the vehicle and the road. For a flat surface, the normal force is the vehicle mass m times the standard gravity g.
![]()
In the case of a road with an inclination angle, the normal force becomes the weight m.g multiplied by the cosine of the road angle. It is important to note that the rolling resistance force is independent of the vehicle speed, and it is always opposite the driving direction. The coefficient Cr should be low so as to keep the frictional losses low. For modern cars, it’s typically around 0.01 to 0.02.
Aerodynamic drag force
As the vehicle speed increase, the aerodynamic drag force opposes the vehicle motion as the air as is forced to flow around the moving vehicle. It can be calculated as the product of the aerodynamic drag coefficient Cd the front area of the vehicle Af, the air density and the square of the vehicle speed v, divided by 2.
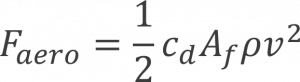
It is hence important to note that the aerodynamic drag in independent of vehicle mass but has a strong dependence on the vehicle speed. That is why in a car, the aerodynamic drag force is higher than the rolling resistance force when the speed is above about 70 to 80 km/h.
Secondly, the coefficient of drag is typically about 0.25 to 0.35 for a modern car. SUVs, with their typically boxy shapes, have coefficients in the range of 0.35 to 0.45.
Gradient force
The third force that acts on a vehicle is the gradient force, and it occurs when the vehicle is driving on an uphill or a downhill road. The gradient force is due to the longitudinal component of gravitational force, namely mg where theta is the inclination angle of the road. As seen earlier, the cosine component of the gravity contributes to the normal force and the corresponding rolling resistance force.
The gradient force and the angle theta are negative when driving downhill, and positive when driving uphill. Road gradients are expressed as a percentage in terms of tangent theta and have a value typically between plus or minus 10%.
If we now consider a vehicle moving on an inclined surface, then the aerodynamic drag force, the rolling resistance force and the gradient force act on the vehicle. If we now include the traction force provided by the vehicle powertrain, then the net force on the vehicle, is the difference between the traction force and the sum of the forces due to the aerodynamic drag, the rolling resistance, and the road gradient.
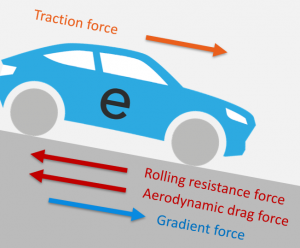
By Newton’s second law, the net force is equal to the product of the vehicle mass and vehicle acceleration. Therefore, we can control the vehicle acceleration and thereby the speed by controlling the traction force that the powertrain produces. The traction force is in the driving direction most of the time, but it can be zero when the vehicle is coasting or even negative when the powertrain is under regenerative braking.
If we now expand the equation for the traction force, we can see the factors that influence the vehicle forces: the vehicle mass and road angle affects the rolling resistance and gradient force, vehicle speed decides the aerodynamic drag force, and the rest of the traction force decides the vehicle acceleration. If we need to estimate the power delivered by the powertrain, then we need to multiply the traction force with the speed of the vehicle.
![]()
It is important to realize that in this lecture, we only take into account the forces in the forward and reverse direction, as they influence the powertrain. The forces in other directions are neglected for simplicity. Secondly, the forces in the vehicle are assumed to be acting at one point. In reality, the forces are distributed over the vehicle.
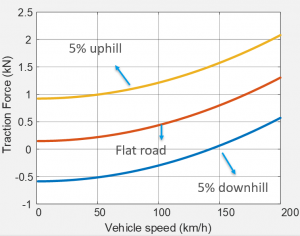
Let us now look at a force/speed diagram of a vehicle with a mass of 1.5 ton, frontal area of 2.5m^2 and the speed range of 0-200 km/h. From the formula for the traction force, we can calculate the force at each speed level for zero vehicle acceleration. Those points make a force/speed curve of this car. When the speed is close to zero, then the traction force is used to overcome the rolling resistance force. As the speed increase, the traction force needed increases fast, as the aerodynamic force increase with the square of the speed.
Next, let us investigate 3 road conditions, a flat road, a 5% gradient uphill, and a 5% gradient downhill. We can see in the downhill condition, the traction force needed for low speeds is negative, as the gradient force is larger than combined rolling resistance and aerodynamic drag forces. On the other hand, the uphill gradient requires a significantly higher traction force for the same speed than the 0% or downhill gradient.
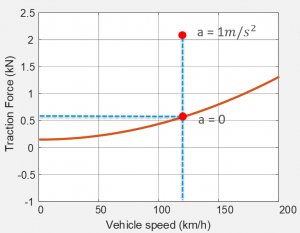
Finally, let’s consider the case when the vehicle has a finite acceleration. This is the speed/force curve for the same car with 0% gradient and zero acceleration. Since the mass of the car is 1500kg, for every 1m/s2 acceleration, an extra 1500N traction force from the powertrain would be required.
Besides the traction force, the EV battery also provides power for the vehicle auxiliaries, like heating, air conditioning, lighting, wiper etc. Hence, the net power delivered by the traction battery, Pbatt is the sum of the traction power and the auxiliary power.
To conclude, the forces acting on a vehicle when it’s driving consist of the rolling resistance force, the aerodynamic drag force and the gradient force. The drive train provides the traction force, which can be controlled to change the vehicle acceleration and hence the speed.

Electric Cars: Technology by TU Delft OpenCourseWare is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
Based on a work at https://online-learning.tudelft.nl/courses/electric-cars-technology/.



