Important announcement

Dear visitor,

Please note that this OpenCourseWare platform will be replaced at the end of 2026 by a new platform (under the same url ocw.tudelft.nl).

Courses and their contents that are currently available the platform will partly be migrated. URL’s for this content will change and content might be unavailable for some time. In addition, some courses will not be available anymore.

If you are linking to specific courses on this platform (for instance for your students), please take timely measures to avoid problems with access. Possible actions are:

  • Download the materials to your local platform (laptop, server)
  • For educators only (including TU Delft lecturers): Contact us at ocw@tudelft.nl and inform us what course you are using in what context (institute, program, period of use, number of students). We will research (in collaboration with the authors of the course) and decide if we will migrate the course, and if yes, can supply you with a new url.

Thank you.

Home Courses Aerospace Mechanics of Materials Course materials Readings Torsion: Angle of Twist

Torsion: Angle of Twist

Course subject(s) 3. Torsion

Derivation of the angle of twist for a thin-walled closed section shaft requires the application of energy methods beyond the scope of the current course. However, it is still necessary to be able to calculate this angle of twist in order to meet the learning objectives of this course (solve statically indeterminate problems containing thin-walled shafts). As a result, the following equation for angle of twist in a uniform thin-walled torsional shaft is provided to you:

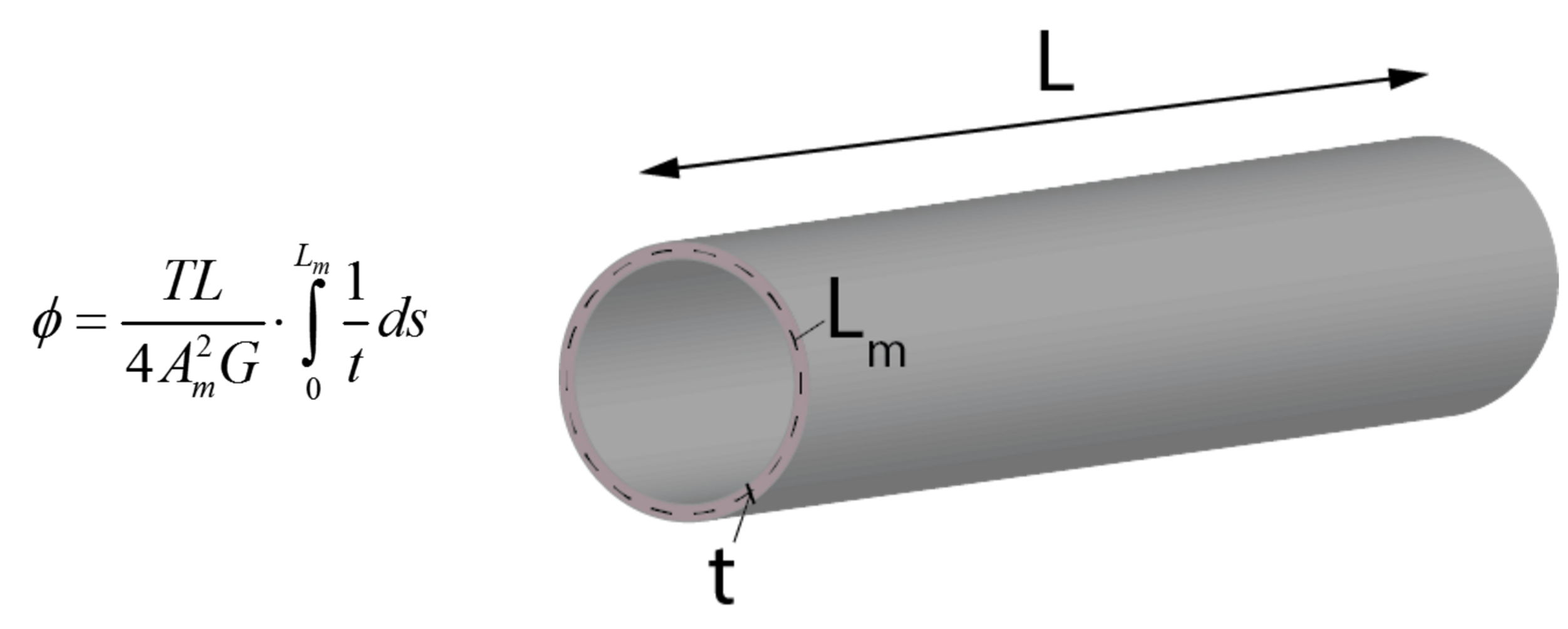
Here, Phi is the angle of twist, Am is the area enclosed by the median line of the cross-section, Lm is the length (perimeter) of the median line, and ds is a differential increment along the median line. Please note that the equation contains an integral that needs to be performed around the preimeter of the cross-section median line.

Creative Commons License
Aerospace Mechanics of Materials by TU Delft OpenCourseWare is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
Based on a work at https://ocw.tudelft.nl/courses/aerospace-mechancis-of-materials/.
Back to top
[sg_popup id=6]