Fill Factor and Open-Circuit Voltage

The fill factor \(FF\) is defined as:

\(FF = \frac{J_{mp}*V_{mp}}{J_{sc}*V_{oc}}\tag{1} \)

where:

• \(J_{mp}\): current density at maximum power point
• \(V_{mp}\): voltage at maximum power point
• \(J_{sc}\): short-circuit current density
• \(V_{oc}\): open-circuit voltage

The maximum power produced by a solar cell occurs at the point where:

\( \frac{dP}{dV}=0 \) or in other words \( \frac{d}{dV}[J(V)*V]=0\) \( \tag{2}\)

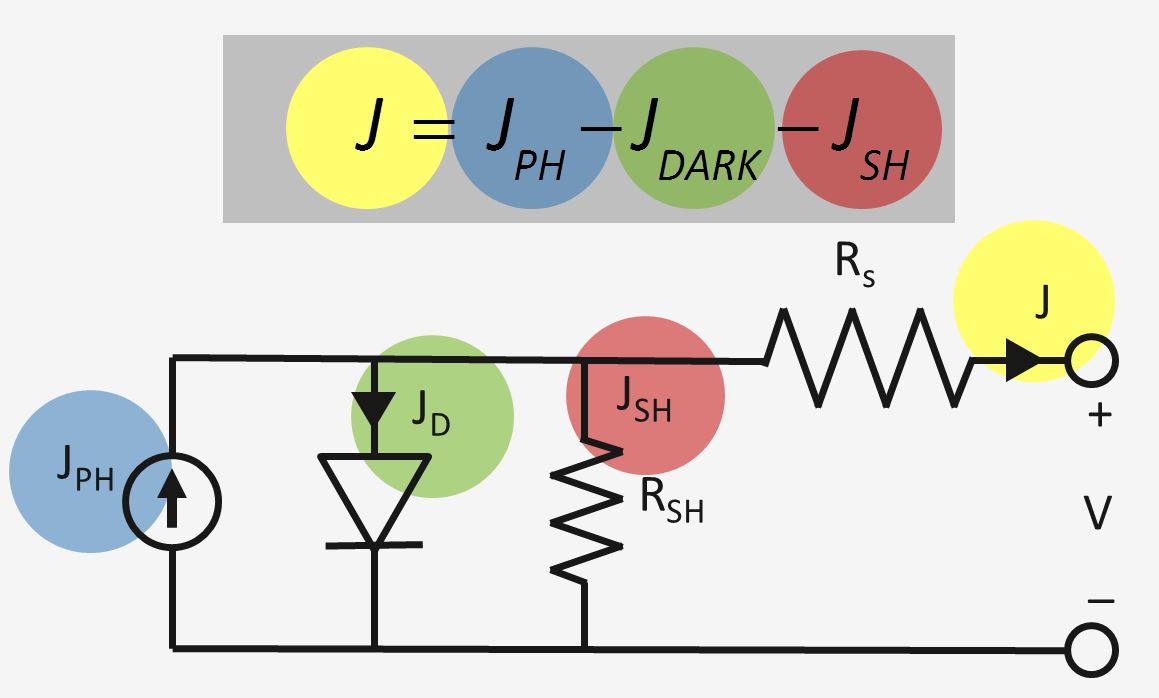
Recall also from video block 3.1 10:03 that: \( J(V)= J_{ph}- J_o[exp(\frac{q*V}{n*k_B*T}) -1] \tag{3}\) where:

• \(k_B\): Boltzmann constant
• \(q\): elementary charge
• \(n\): ideality factor, which for this course is considered as 1
• \(T\): operating temperature

Therefore we can write that: \( \frac {d}{dV} \Big\{\big[J_{ph}- J_o(exp(\frac{q*V}{n*k_B*T}) -1)\big]*V\Big\} \Bigg|_{V=V_{mp}} =0 \tag{4} \)

Let \( \alpha=\frac{q}{n*k_B*T} \)

The above equation can be written as:

\( \frac {d}{dV} \Big\{\big[J_{ph}- J_o(exp(\alpha*V)-1)\big]*V\Big\} \Bigg|_{V=V_{mp}} =0 \tag{5}\)

Working out equation \((5)\) we can derive the relationship: \( \frac {J_{ph}}{J_o}+1=exp(\alpha*V_{mp})*(1+\alpha* V_{mp}) \tag{6}\)

However the \(V_{oc} \) is: \( V_{oc}=\frac {n*k*T}{q}*ln(\frac {J_{ph}}{J_o}+1) \tag{7}\)

which by replacing the term \( \frac {n*k_B*T}{q} \) becomes: \( V_{oc}=\frac {1}{\alpha}*ln(\frac {J_{ph}}{J_o}+1) \tag{8} \)

Taking the natural logarithm at both sides of equation \((6)\) and using \((8)\), we can derive: \( V_{mp}=V_{oc}-\frac {1}{\alpha}*ln(1+\alpha*V_{mp}) \tag{9} \)

Equation \((9)\) does not have an analytical solution. That means that we cannot solve \((9)\) for \( V_{mp} \).

If we replace equation \((9)\) into equation \((1)\), we also notice that we cannot derive an analytical solution for \(FF\) and \(V_{oc}\).

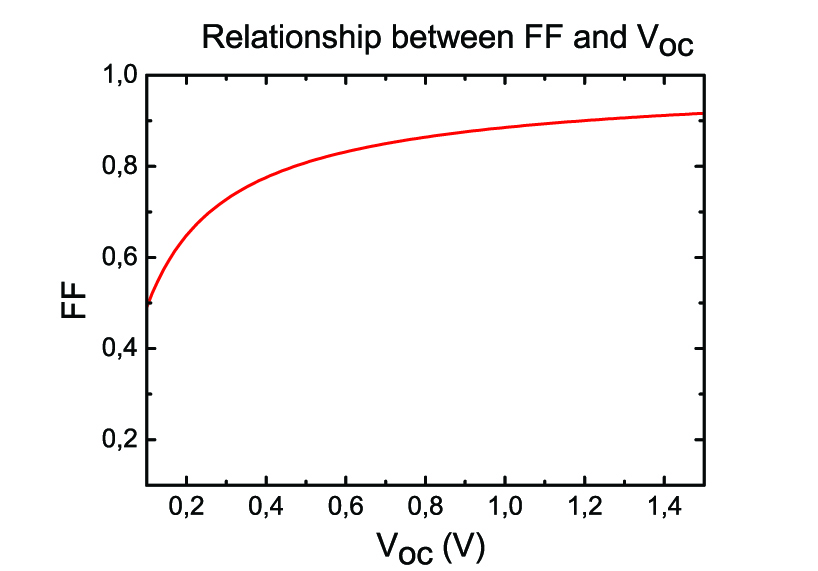
An empirical relationship of \( FF \) and \(V_{oc}\) is the following: \( FF= \frac {{ \alpha}*V_{oc}-ln( {\alpha}*V_{oc}+0.72)}{{\alpha}*V_{oc}+1} \tag{10}\)

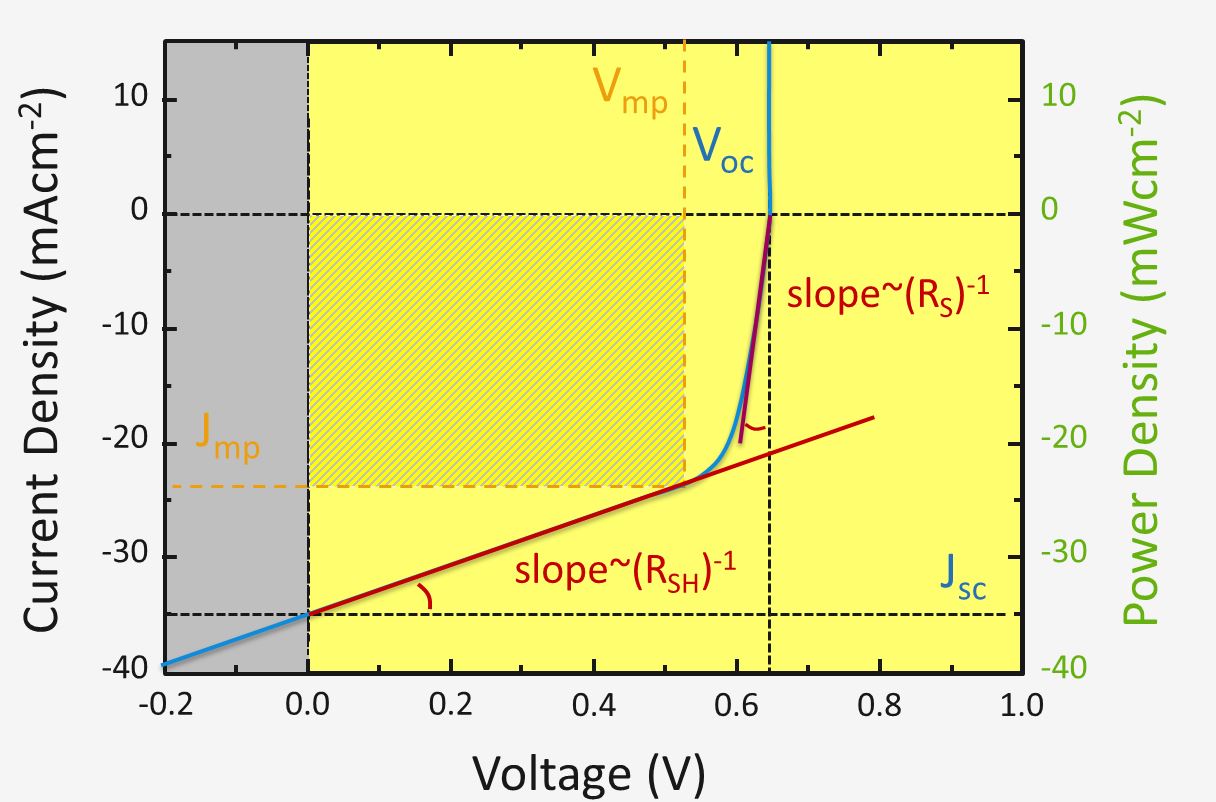
In the figure on the right the J-V curve of a non-ideal p-n junction is shown.

We are going to show that a fairly good estimation of the series resistance \(R_s\) can be made by finding the slope \( dJ/dV \) at the open-circuit voltage point \(V_{oc}\). Similarly we are going to show that the shunt resistance \(R_{sh}\) can be estimated from the slope \( dJ/dV \) at the short-circuit point \(J_{sc}\).